题目内容
在二项式 的展开式中,若前3项的系数成等差数列,则展开式中有理项的项数为
的展开式中,若前3项的系数成等差数列,则展开式中有理项的项数为
- A.5
- B.4
- C.3
- D.2
C
分析:利用二项展开式的通项公式求出展开式的通项,求出前三项的系数,利用等差数列得到关于n的等式,求出n的值,将n的值代入通项,令x的指数为整数,得到r的值,得到展开式中有理项的项数.
解答:解;展开式的通项
前三项的系数分别为1,
∵前3项的系数成等差数列
∴ 解得n=8
解得n=8
∴展开式的通项为
要项为有理项,需x的指数为整数
∴r=0,4,8为有理项
故选C
点评:求二项展开式的特定项问题,一般利用的工具是二项展开式的通项公式.
分析:利用二项展开式的通项公式求出展开式的通项,求出前三项的系数,利用等差数列得到关于n的等式,求出n的值,将n的值代入通项,令x的指数为整数,得到r的值,得到展开式中有理项的项数.
解答:解;展开式的通项

前三项的系数分别为1,

∵前3项的系数成等差数列
∴
 解得n=8
解得n=8∴展开式的通项为

要项为有理项,需x的指数为整数
∴r=0,4,8为有理项
故选C
点评:求二项展开式的特定项问题,一般利用的工具是二项展开式的通项公式.

练习册系列答案
相关题目


 的展开式中,含
的展开式中,含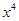 的项的系数是
的项的系数是  的展开式中,含
的展开式中,含 的项的系数是
的项的系数是