题目内容
定义在R上的偶函数 满足
满足 ,且在[-1,0]上单调递增,设
,且在[-1,0]上单调递增,设 ,
,  ,
, ,则
,则 大小关系是( )
大小关系是( )
A. | B. | C.  | D. |
A
解析试题分析:根据题意,由于在R上的偶函数 满足
满足 ,则f(x+2)=f(x),且在[-1,0]上单调递增,在[0,1]上递减 函数,则可知函数的
,则f(x+2)=f(x),且在[-1,0]上单调递增,在[0,1]上递减 函数,则可知函数的 ,
,  ,
, ,则根据函数的单调性可知
,则根据函数的单调性可知 ,选A.
,选A.
考点:函数的奇偶性以及单调性
点评:主要是考查了函数的性质的简答运用,属于基础题。

练习册系列答案
相关题目
给出下列函数① ②
② ③
③ ④
④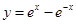 ,其中是奇函数的是( )
,其中是奇函数的是( )
| A.①② | B.①④ | C.②④ | D.③④ |
定义在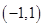 上的函数
上的函数 是奇函数,并且在
是奇函数,并且在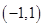 上
上 是减函数,求满足条件
是减函数,求满足条件 的
的 取值范围.( )
取值范围.( )
A. | B. | C. | D. |
函数 ( )
( )
| A.增函数 | B.减函数 | C.不具备单调性 | D.无法判断 |
设定义在 上的奇函数
上的奇函数 ,满足对任意
,满足对任意 都有
都有 ,且
,且 时,
时, ,则
,则 的值等于( )
的值等于( )
A. | B. | C.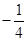 | D. |
若函数 在
在 处取最小值, 则
处取最小值, 则 =( )
=( )
A.1+ | B.1+ | C.3 | D.4 |
已知函数 满足对任意实数
满足对任意实数 ,都有
,都有 成立,则实数
成立,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
下列函数中,既是偶函数又在区间 上单调递减的是( )
上单调递减的是( )
A. | B. | C. | D. |
 ,符号
,符号 表示不超过
表示不超过 的最大整数,若函数
的最大整数,若函数 有且仅有3个零点,则
有且仅有3个零点,则 的取值范围是( )
的取值范围是( )


