题目内容
、
异面直线，
为空间任一点，过作直线
与、均相交，这样的直线可以作多少条。
，
或无数
解析:
过存在唯一个平面
过存在唯一个平面
① 若
或
，有无数条
② 若
或，且
且
直线不存在
③ 
且
，有且只有一条。
，过、作平面
∴ 
∴ 
连
与相交
∴ 存在与、均相交
假设有两条过的直线
、
与、均相交
，确立平面
与、各有一个交点
∴ 
同理
，与、异面矛盾
∴ 假设不成立
∴ 只有一条
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
//平面
，
是夹在
间的线段，若
//
，则
；
是异面直线，
是异面直线，则
一定是异面直线；
，
//
；
到三角形三个顶点的距离相等，则点
是两条异面直线，
//平面
，
是夹在
间的线段，若
//
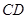，则
；
是异面直线，
是异面直线，则
一定是异面直线；
，
//
；
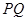到三角形三个顶点的距离相等，则点
是两条异面直线，
、
异面直线，
为空间任一点，过
与