Question

（本小题满分12分）如图，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=，BC=1，PA=2，E为PD的中点．
（1）求直线AC与PB所成角的余弦值；
（2）在侧面PAB内找一点N，使NE⊥面PAC，并求出N点到AB和AP的距离．

Answer 1

解：（1）设AC∩BD=O，连OE，则OE//PB，∴∠EOA即为AC与PB所成的角或其补角.在△AOE中，AO=1，OE=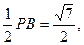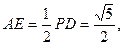∴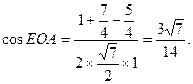即AC与PB所成角的余弦值为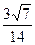.      ---------6分
（2）在面ABCD内过D作AC的垂线交AB于F，则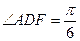.连PF，则在Rt△ADF中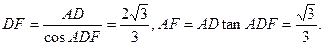设N为PF的中点，连NE，则NE//DF，
∵DF⊥AC，DF⊥PA，∴DF⊥面PAC，从而NE⊥面PAC.∴N点到AB的距离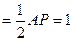，N点到AP的距离 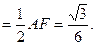          -------------12分
用向量法做对同样给分

解析