题目内容
已知直三棱柱ABC-A1B1C1中,A1C与底面ABC所成的角为![]() ,AB=BC=
,AB=BC=![]() ,∠ABC=
,∠ABC=![]() ,设E、F分别是AB、A1C的中点。
,设E、F分别是AB、A1C的中点。

(1)求证:BC⊥A1E;
(2)求证:EF∥平面BCC1B1;
(3)求以EC为棱,B1EC与BEC为面的二面角正切值。
证法一:向量法
证法二:(I)由已知有BC⊥AB,BC⊥B1B,∴BC⊥平面ABB1A1
又A1E在平面ABB1A1内 ∴有BC⊥A1E
(II)取B1C的中点D,连接FD、BD
∵F、D分别是AC1、B1C之中点, ∴FD![]()
![]() A1B1
A1B1![]() BE
BE
∴四边形EFBD为平行四边形 ∴EF![]() BD
BD
又BD![]() 平面BCC1B1
平面BCC1B1
∴EF∥面BCC1B1
(Ⅲ)过B1作B1H⊥CEFH,连BH,又B1B⊥面BAC,B1H⊥CE
∴BH⊥EC ∴∠B1HB为二面角B1-EC-B平面角
在Rt△BCE中有BE=![]() ,BC=
,BC=![]() ,CE=
,CE=![]() ,BH=
,BH=![]()
又∠A1CA=![]() ∴BB1=AA1=AC=2
∴BB1=AA1=AC=2
∴tan∠B1HB=![]() .
.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.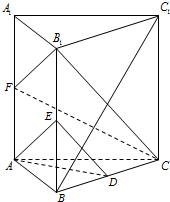 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.