题目内容
（14分）如图，在三棱锥
中，
平面
，
，
，D为BC的中点．
（1）判断AD与SB能否垂直，并说明理由；
（2）若三棱锥的体积为
，且
为
钝角，求二面角
的平面角的正切值；
（3）在（Ⅱ）的条件下，求点A到平面SBC的距离．
解：（1）因为SB在底面ABC上的射影AB与AD不垂直，否则与AB=AC且D为BC的中点矛盾，所以AD与SB不垂直；（4分）
（2）设
，则
解得 
，所以
（舍），
．
平面ABC，AB=AC，D为BC的中点
，
则
是二面角S—BC—A的平面角．
在
中，
,
故二面角的正切值为４；（9分）
（3）由（2）知，
平面SDA，所以平面SBC
平面SDA，过点A作AESD，则AE平面SBC，于是点A到平面SBC的距离为AE,
从而
即A到平面SBC的距离为
．（14分）
练习册系列答案
相关题目
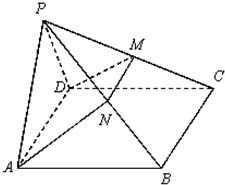如图，在四棱锥P-ABCD中，侧面PAD是正三角形，且与底面ABCD垂直，底面ABCD是边长为2的菱形，∠BAD=60°，N是PB中点，过A、N、D三点的平面交PC于M．
（2013•青岛一模）如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，N是PB中点，过A、N、D三点的平面交PC于M．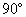
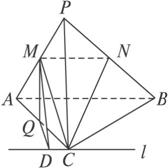
，∠B=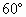
，PC⊥平面ABC，AB=8，PC=6，M，N分别是PA，PB的中点，设△MNC所在平面与△ABC所在平面交于直线l．(1)判断l与MN的位置关系；(2)求点M到l的距离．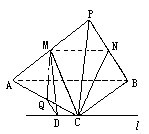
如图，在四棱锥
中，侧面
垂直，底面
，
是
中点，过
、
三点的平面交
于
． 
； (2)求证：
中点；(3)求证：平面
⊥平面
.