题目内容
某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s.已知各观测点到该中心的距离都是1020m.试确定该巨响发生的位置.(假定当时声音传播的速度为340m/s:相关各点均在同一平面上)分析:以接报中心为原点O,正东、正北方向为x轴、y轴正向,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(-1020,0),B(1020,0),C(0,1020),P(x,y)为巨响为生点,由双曲线定义知P点在以A、B为焦点的双曲线
-
=1上,依题意能求出双曲线方程,从而确定该巨响发生的位置.
| x2 |
| a2 |
| y2 |
| b2 |
解答: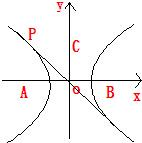 解:如图,
解:如图,
以接报中心为原点O,正东、正北方向为x轴、y轴正向,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(-1020,0),B(1020,0),C(0,1020)
设P(x,y)为巨响为生点,由A、C同时听到巨响声,得|PA|=|PC|,故P在AC的垂直平分线PO上,PO的方程为y=-x,因B点比A点晚4s听到爆炸声,故|PB|-|PA|=340×4=1360
由双曲线定义知P点在以A、B为焦点的双曲线
-
=1上,
依题意得a=680,c=1020,∴b2=c2-a2=10202-6802=5×3402
故双曲线方程为
-
=1
用y=-x代入上式,得x=±680
,
∵|PB|>|PA|,
∴x=-680
,y=680
,即P(-680
,680
),故PO=680
答:巨响发生在接报中心的西偏北450距中心680
m处.
 解:如图,
解:如图,以接报中心为原点O,正东、正北方向为x轴、y轴正向,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(-1020,0),B(1020,0),C(0,1020)
设P(x,y)为巨响为生点,由A、C同时听到巨响声,得|PA|=|PC|,故P在AC的垂直平分线PO上,PO的方程为y=-x,因B点比A点晚4s听到爆炸声,故|PB|-|PA|=340×4=1360
由双曲线定义知P点在以A、B为焦点的双曲线
| x2 |
| a2 |
| y2 |
| b2 |
依题意得a=680,c=1020,∴b2=c2-a2=10202-6802=5×3402
故双曲线方程为
| x2 |
| 6802 |
| y2 |
| 5×3402 |
用y=-x代入上式,得x=±680
| 5 |
∵|PB|>|PA|,
∴x=-680
| 5 |
| 5 |
| 5 |
| 5 |
| 10 |
答:巨响发生在接报中心的西偏北450距中心680
| 10 |
点评:本题考查双曲线的性质和应用,解题时由题设条件作出图形,数形结合效果很好.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目