题目内容
设等比数列 中,前n项和为
中,前n项和为 ,已知
,已知 =8,
=8, =7,则
=7,则 等于( )
等于( )
A. | B.- | C. | D. |
A.
解析试题分析:利用等比数列的性质:若{an}为等比数列,则 , 也成等比数列.
, 也成等比数列. 解得
解得 ,
, .
.
考点:等比数列的前 项和;等比数列的通项公式.
项和;等比数列的通项公式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
在数列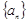 中,已知
中,已知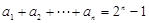 ,则
,则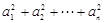 等于 ( )
等于 ( )
A.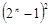 | B.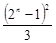 | C.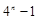 | D.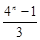 |
在等比数列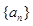 中,若
中,若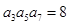 ,则
,则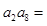 ( )
( )
| A.4 | B.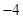 | C.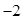 | D.2 |
在等比数列 中,
中, ,则公比
,则公比 的值为
的值为
A. | B. | C. | D. |
一无穷等比数列 各项的和为
各项的和为 ,第二项为
,第二项为 ,则该数列的公比为 ( )
,则该数列的公比为 ( )
A. | B. | C. | D. 或 或 |
在等比数列 中,如果
中,如果 ,那么
,那么 等于( )
等于( )
| A.2 | B. | C. | D.4 |
已知等比数列{an}满足an>0,n∈N*,且a5·a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( )
| A.n(2n-1) | B.(n+1)2 | C.n2 | D.(n-1)2 |
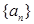 是等差数列,且
是等差数列,且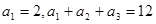 .
.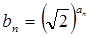 ,求数列
,求数列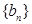 的前10项和.
的前10项和. 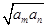 =4a1,则
=4a1,则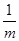 +
+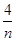 的最小值为________.
的最小值为________.