题目内容
设函数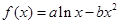 ,
,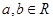 (1)若函数
(1)若函数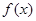 在
在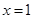 处与直线
处与直线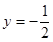 相切;
相切;
(1) ①求实数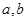 的值; ②求函数
的值; ②求函数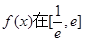 上的最大值;
上的最大值;
(2)当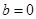 时,若不等式
时,若不等式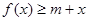 对所有的
对所有的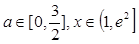 都成立,求实数
都成立,求实数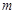 的取值范围.
的取值范围.
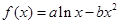 ,
,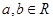 (1)若函数
(1)若函数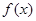 在
在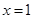 处与直线
处与直线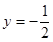 相切;
相切;(1) ①求实数
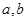 的值; ②求函数
的值; ②求函数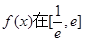 上的最大值;
上的最大值;(2)当
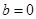 时,若不等式
时,若不等式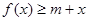 对所有的
对所有的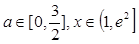 都成立,求实数
都成立,求实数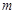 的取值范围.
的取值范围.(1)①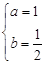 ②
②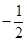 (2)
(2)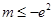
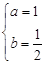 ②
②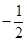 (2)
(2)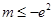
本试题主要是考查了导数在研究函数中的运用。
(1)根据导数的几何意义得到解析式。
(2)求解导函数,然后根据导数的正负号与单调性的关系得到极值和最值。
(3)要证明不等式恒成立,转换为研究函数的最值问题,构造函数求解得到结论。
解:(1)①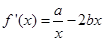 ∵函数
∵函数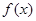 在
在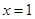 处与直线
处与直线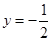 相切
相切
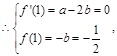 解得
解得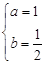
②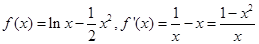
当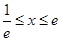 时,令
时,令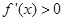 得
得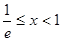 ;
;
令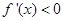 ,得
,得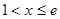
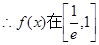 上单调递增,在[1,e]上单调递减,
上单调递增,在[1,e]上单调递减,
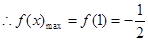 …………6分
…………6分
(2)当b=0时,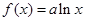 若不等式
若不等式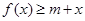 对所有的
对所有的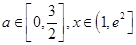 都成立,
都成立,
则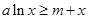 对所有的
对所有的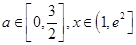 都成立,
都成立,
即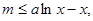 对所有的
对所有的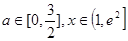 都成立,
都成立,
令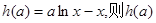 为一次函数,
为一次函数,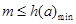
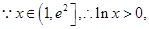
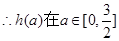 上单调递增
上单调递增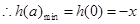 ,
,
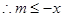 对所有的
对所有的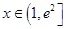 都成立。
都成立。
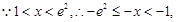
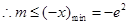
(1)根据导数的几何意义得到解析式。
(2)求解导函数,然后根据导数的正负号与单调性的关系得到极值和最值。
(3)要证明不等式恒成立,转换为研究函数的最值问题,构造函数求解得到结论。
解:(1)①
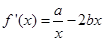 ∵函数
∵函数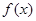 在
在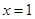 处与直线
处与直线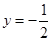 相切
相切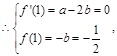 解得
解得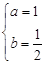
②
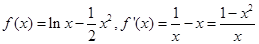
当
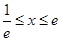 时,令
时,令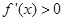 得
得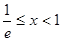 ;
;令
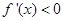 ,得
,得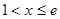
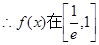 上单调递增,在[1,e]上单调递减,
上单调递增,在[1,e]上单调递减,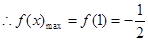 …………6分
…………6分(2)当b=0时,
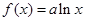 若不等式
若不等式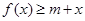 对所有的
对所有的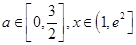 都成立,
都成立,则
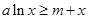 对所有的
对所有的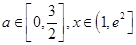 都成立,
都成立,即
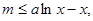 对所有的
对所有的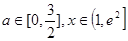 都成立,
都成立,令
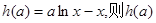 为一次函数,
为一次函数,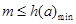
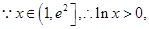
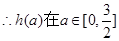 上单调递增
上单调递增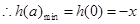 ,
,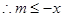 对所有的
对所有的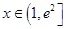 都成立。
都成立。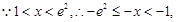
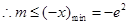

练习册系列答案
相关题目
 图象上一点
图象上一点 处
处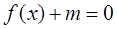 在
在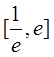 内有两个不等实根,求m的取值范围(其
内有两个不等实根,求m的取值范围(其 为自然对数的底数);
为自然对数的底数);
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数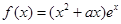 ,其中
,其中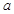 为正实数,
为正实数,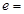 2.7182……
2.7182……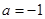 时,求
时,求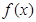 在点
在点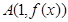 处的切线方程。
处的切线方程。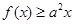 恒成立。
恒成立。 在点
在点 处的切线方程是 。
处的切线方程是 。 =
= (
(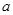 为实常数).
为实常数).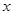 =1处与
=1处与 ],使得
],使得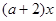 成立,求实数
成立,求实数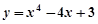 在区间
在区间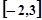 上的最小值为( )
上的最小值为( )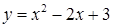 在点(2,3)处的切线方程为( )
在点(2,3)处的切线方程为( )


