题目内容
数列an满足a1=2，an+1=an+2n，则通项公式an=________，前n项和Sn=________．
2n 2n+1-2
分析：利用递推关系一步步地把通项用首项和关于n的表达式表示出来，即可求得an．再代入求和公式即可求sn
解答：由题得，an=an-1+2n-1=an-2+2n-2+2n-1=an-3+2n-3+2n-2+2n-1=…=a1+21+22+…+2n-1=2+
=2n．
所以前n项和Sn=21+22+23+…+2n=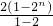
=2n+1-2．
故答案为：2n，2n+1-2．
点评：本题是对递推关系式和等比数列求和公式的综合考查．在利用等比数列的求和公式时，一定要先看公比的取值，再代入公式．
分析：利用递推关系一步步地把通项用首项和关于n的表达式表示出来，即可求得an．再代入求和公式即可求sn
解答：由题得，an=an-1+2n-1=an-2+2n-2+2n-1=an-3+2n-3+2n-2+2n-1=…=a1+21+22+…+2n-1=2+
=2n．所以前n项和Sn=21+22+23+…+2n=
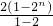=2n+1-2．故答案为：2n，2n+1-2．
点评：本题是对递推关系式和等比数列求和公式的综合考查．在利用等比数列的求和公式时，一定要先看公比的取值，再代入公式．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目