题目内容
记函数f(x)=x2-2ax+1在x∈[-1,1]上的最大值为g(a).(Ⅰ)求g(a);
(Ⅱ)作出函数y=g(a)的图象.
分析:(Ⅰ)把f(x)的解析式化为顶点形式后,找出对称轴为直线x=a,然后找出区间的中点为0,分a大于等于0和a小于0两种情况,分别求出g(a),即可得到g(a)关于a的分段函数关系式;
(Ⅱ)利用画函数图象的步骤:列表,描点和连线,根据g(a)的解析式即可画出函数的图象.
(Ⅱ)利用画函数图象的步骤:列表,描点和连线,根据g(a)的解析式即可画出函数的图象.
解答:解:(Ⅰ)f(x)=x2-2ax+1=(x-a)2+1-a2,
当a≥0时,g(a)=f(-1)=2+2a;
当a<0时,g(a)=f(1)=2-2a;
∴g(a)=
;
(Ⅱ)由g(a)=
列出表格如下:

作出g(a)的图象如图所示:
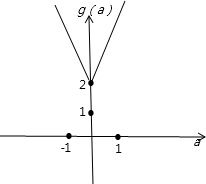
当a≥0时,g(a)=f(-1)=2+2a;
当a<0时,g(a)=f(1)=2-2a;
∴g(a)=
|
(Ⅱ)由g(a)=
|
列出表格如下:

作出g(a)的图象如图所示:

点评:此题考查学生掌握二次函数的图象与性质,会利用描点法画出分段函数的图象,是一道综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目