Question

【题目】如图，平行四边形ABCD中，CD=1，∠BCD=60°，BD⊥CD，正方形ADEF，且面ADEF⊥面ABCD．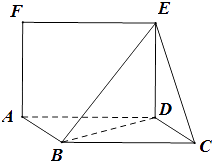
（Ⅰ）求证：BD⊥平面ECD．
（Ⅱ）求D点到面CEB的距离．

Answer 1

【答案】证明：（I）∵四边形ADEF为正方形， ∴ED⊥AD，
又∵平面ADEF⊥平面ABCD，平面ADEF∩平面ABCD=AD，
∴ED⊥平面ABCD，∴ED⊥BD．
又∵BD⊥CD，ED∩CD=D，
∴BD⊥平面ECD．
（ II）解：∵CD=1，∠BCD=60°，BD⊥CD，
又∵正方形ADEF，∴CB=2，CE= ， ，
∴ ，∴ ，
Rt△BCD的面积等于 S△BCD= 1 = ，
由得（ I）ED⊥平面ABCD，∴点E到平面BCD的距离为ED=2，设点D到到面CEB的距离为h，
∴ = ，∴h= ，
即点D到到面CEB的距离为 ．
【解析】（ I）由条件证明ED⊥BD，再根据BD⊥CD，利用直线和平面垂直的判定定理证得BD⊥平面ECD． II）先求△CBE的面积，Rt△BCD的面积，设点D到到面CEB的距离为h，利用等体积法求点D到平面CBE的距离h的值．
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点，需要掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题．