题目内容
(满分17分)
已知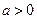 ,函数
,函数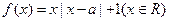 .
.
(1)当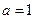 时,求所有使
时,求所有使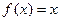 成立的
成立的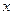 的值;
的值;
(2)当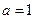 时,求函数
时,求函数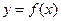 在闭区间
在闭区间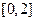 上的最大值和最小值;
上的最大值和最小值;
(3) 试讨论函数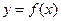 的图像与直线
的图像与直线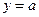 的交点个数.
的交点个数.
已知
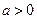 ,函数
,函数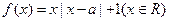 .
.(1)当
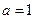 时,求所有使
时,求所有使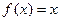 成立的
成立的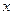 的值;
的值;(2)当
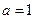 时,求函数
时,求函数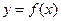 在闭区间
在闭区间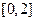 上的最大值和最小值;
上的最大值和最小值;(3) 试讨论函数
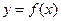 的图像与直线
的图像与直线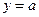 的交点个数.
的交点个数.(1)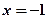 或
或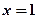 ;
;
(2)函数的最大值为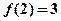 ,最小值为
,最小值为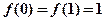
(3)当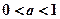 时,函数
时,函数 的图像与直线
的图像与直线 有1个交点;
有1个交点;
当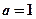 时,函数
时,函数 的图像与直线
的图像与直线 有2个交点;
有2个交点;
当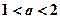 时,函数
时,函数 的图像与直线
的图像与直线 有3个交点;
有3个交点;
当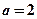 时,函数
时,函数 的图像与直线
的图像与直线 有2个交点;
有2个交点;
当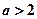 时,函数
时,函数 的图像与直线
的图像与直线 有3个交点
有3个交点
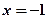 或
或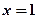 ;
;(2)函数的最大值为
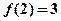 ,最小值为
,最小值为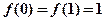
(3)当
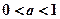 时,函数
时,函数 的图像与直线
的图像与直线 有1个交点;
有1个交点;当
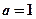 时,函数
时,函数 的图像与直线
的图像与直线 有2个交点;
有2个交点;当
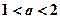 时,函数
时,函数 的图像与直线
的图像与直线 有3个交点;
有3个交点;当
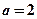 时,函数
时,函数 的图像与直线
的图像与直线 有2个交点;
有2个交点;当
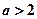 时,函数
时,函数 的图像与直线
的图像与直线 有3个交点
有3个交点(1)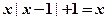
所以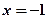 或
或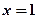 ;....................................5分
;....................................5分
(2)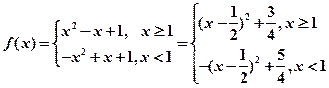 ....................7分
....................7分
结合图像可知函数的最大值为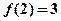 ,最小值为
,最小值为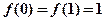 ..............10分
..............10分
(3)因为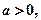 所以
所以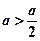 ,
,
所以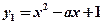 在
在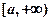 上递增;.....................................12分
上递增;.....................................12分
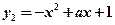 在
在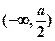 递增,在
递增,在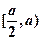 上递减............................13分
上递减............................13分
因为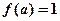 ,所以当
,所以当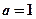 时,函数
时,函数 的图像与直线
的图像与直线 有2个交点;
有2个交点;
又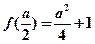 ,而
,而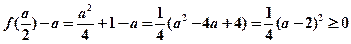 ,
,
当且仅当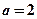 时,上式等号成立.........................................15分
时,上式等号成立.........................................15分
所以,当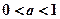 时,函数
时,函数 的图像与直线
的图像与直线 有1个交点;
有1个交点;
当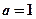 时,函数
时,函数 的图像与直线
的图像与直线 有2个交点;
有2个交点;
当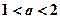 时,函数
时,函数 的图像与直线
的图像与直线 有3个交点;
有3个交点;
当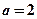 时,函数
时,函数 的图像与直线
的图像与直线 有2个交点;
有2个交点;
当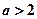 时,函数
时,函数 的图像与直线
的图像与直线 有3个交点.................17分
有3个交点.................17分
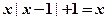
所以
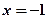 或
或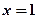 ;....................................5分
;....................................5分(2)
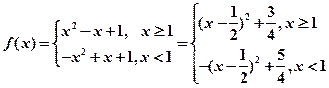 ....................7分
....................7分结合图像可知函数的最大值为
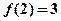 ,最小值为
,最小值为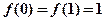 ..............10分
..............10分(3)因为
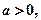 所以
所以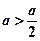 ,
,所以
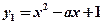 在
在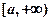 上递增;.....................................12分
上递增;.....................................12分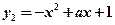 在
在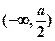 递增,在
递增,在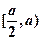 上递减............................13分
上递减............................13分因为
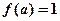 ,所以当
,所以当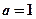 时,函数
时,函数 的图像与直线
的图像与直线 有2个交点;
有2个交点;又
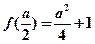 ,而
,而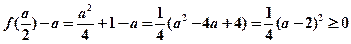 ,
,当且仅当
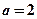 时,上式等号成立.........................................15分
时,上式等号成立.........................................15分所以,当
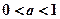 时,函数
时,函数 的图像与直线
的图像与直线 有1个交点;
有1个交点;当
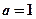 时,函数
时,函数 的图像与直线
的图像与直线 有2个交点;
有2个交点;当
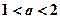 时,函数
时,函数 的图像与直线
的图像与直线 有3个交点;
有3个交点;当
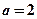 时,函数
时,函数 的图像与直线
的图像与直线 有2个交点;
有2个交点;当
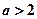 时,函数
时,函数 的图像与直线
的图像与直线 有3个交点.................17分
有3个交点.................17分
练习册系列答案
相关题目
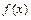 是定义在
是定义在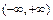 上的增函数,是否存在这样的实数
上的增函数,是否存在这样的实数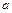 ,使得不等式
,使得不等式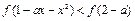 对于任意
对于任意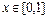 都成立?若存在,试求出实数
都成立?若存在,试求出实数 是定义在
是定义在 上的增函数,函数
上的增函数,函数 的图象关于点
的图象关于点 对称.若实数
对称.若实数 满足不等式
满足不等式 ,则
,则 的取值范围是 .
的取值范围是 . 是定义在实数集
是定义在实数集 上的奇函数,对任意的实数
上的奇函数,对任意的实数 ,当
,当 时,
时, ,则
,则 等于
等于



 满足
满足 ,则
,则 的值为( )
的值为( )
 有关
有关 在(0,+
在(0,+ )上为增函数,且
)上为增函数,且 .那么不等式
.那么不等式 的解集是 ;
的解集是 ; 的解的个数为 ( )
的解的个数为 ( )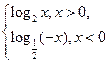 ,若f(a)>f(-a),则实数a的取值范围是( )
,若f(a)>f(-a),则实数a的取值范围是( )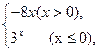 则f[f(
则f[f(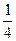 )]的值是 ( )
)]的值是 ( )