题目内容
已知抛物线C的顶点为O(0,0),焦点F(0,1).
(1)求抛物线C的方程.
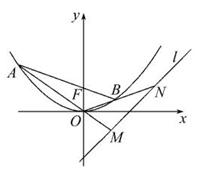
(2)过F作直线交抛物线C于A,B两点.若直线AO,BO分别交直线l:y=x-2于M,N两点,求|MN|的最小值.
【解题提示】(1)知道抛物线的焦点易求抛物线的方程;(2)可以先设出A,B两点的坐标(设而不求),设出直线的方程,由已知条件把|MN|表示出来,进行求解.
【解析】(1)由题意可设抛物线C的方程为x2=2py(p>0),则![]() =1,p=2,
=1,p=2,
所以抛物线C的方程为x2=4y.
(2)设A(x![]() 1,y1),B(x2,y2),
1,y1),B(x2,y2),
直线AB的方程为:y=kx+1,
由![]() 消去y,整理得x2-4kx-4=0,
消去y,整理得x2-4kx-4=0,
所以x1+x2=4k,x1x2=-4,
从而|x1-x2|=4![]() ,
,
由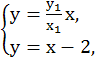 解得点M的横坐标xM=
解得点M的横坐标xM=![]() =
=![]() =
=![]() ,
,
同理点N的横坐标xN=![]() ,
,
所以|MN|=![]() |xM-xN|
|xM-xN|
=![]()
=8![]()
=![]() .
.
令4k-3=t,t≠0,则k=![]() ,
,
当t>0时,|MN|![]() =2
=2![]() >2
>2![]() ,
,
当t<0时,|MN|=2![]()
![]() ≥
≥![]() ,
,
综上所述,当t=-![]() ,即k=-
,即k=-![]() 时,|MN|的最小值是
时,|MN|的最小值是![]() .
.

练习册系列答案
相关题目