题目内容
(满分12分)某次体能测试中,规定每名运动员一开始就要参加且最多参加四次测试.一旦测试通过,就不再参加余下的测试,否则一直参加完四次测试为止.已知运动员甲的每次通过率为 (假定每次通过率相同).
(假定每次通过率相同).
(1) 求运动员甲最多参加两次测试的概率;
(2) 求运动员甲参加测试的次数的分布列及数学期望(精确到0.1).
(1) 因为运动员甲参加一次测试的概率是0.7 ,
运动员甲参加两次测试的概率是0.3×0.7=0.21,
所以运动员甲最多参加两次测试的概率是0.7+0.21=0.91;
(2) 的分布列为:
的分布列为:
|
|
1 |
2 |
3 |
4 |
|
|
0.7 |
0.21 |
0.063 |
0.027 |

 。
。
【解析】(1)解本小题的关键是知道运动员甲最多参加两次测试包括运动员甲参加一次测试和运动员甲参加两次测试并且这两个事件是互斥的.
(II)先确定 的可能取值为
的可能取值为 然后求出每一个值对应的概率,列出分布列,再根据期望公式求值即可.
然后求出每一个值对应的概率,列出分布列,再根据期望公式求值即可.
解:(1) 因为运动员甲参加一次测试的概率是0.7 ………… 1分
运动员甲参加两次测试的概率是0.3×0.7=0.21………… 3分
所以运动员甲最多参加两次测试的概率是0.7+0.21=0.91………4分
(2) 的可能取值为
的可能取值为 ………… 5分
………… 5分
 ;
; ………… 9分
………… 9分
 的分布列为:
的分布列为:
|
|
1 |
2 |
3 |
4 |
|
|
0.7 |
0.21 |
0.063 |
0.027 |
………… 10分

 ………… 12分
………… 12分

(本小题满分14分)
某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,得到如下数据:
| 序 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(厘米) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长y( 码 ) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
| 序 号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(厘米) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y( 码 ) | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
(Ⅰ)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成下面的![]() 联列表:
联列表:
| 高 个 | 非高个 | 合 计 | |
| 大 脚 | |||
| 非大脚 | 12 | ||
| 合 计 | 20 |
(Ⅱ)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为脚的大小与身高之间有关系?
(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:
①抽到12号的概率;②抽到“无效序号(超过20号)”的概率.

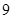 选
选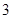 考核(即共
考核(即共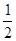 ,第二次参加考试合格的概率为
,第二次参加考试合格的概率为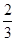 ,第三次参加考试合格的概率为
,第三次参加考试合格的概率为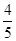 ,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.
,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.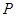 ;
;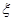 分布列.
分布列.