题目内容
9.若函数f(x)=1og${\;}_{\frac{1}{2}}$(x2-ax+1).(1)若函数的定义域为R,求a的取值范围.
(2)若函数的值域为R,求a的取值范围.
分析 (1)根据题意化为x2-ax+1>0恒成立问题,利用判别式△求出a的取值范围;
(2)根据题意y=x2-ax+1取遍大于0的值,利用判别式△求出a的取值范围.
解答 解:(1)函数f(x)=1og${\;}_{\frac{1}{2}}$(x2-ax+1)的定义域为R,
则x2-ax+1>0在x∈R时恒成立,
∴△<0,即a2-4<0,
解得-2<a<2,
∴实数a的取值范围是(-2,2);
(2)若函数f(x)=1og${\;}_{\frac{1}{2}}$(x2-ax+1)的值域为R,
则△≥0,即a2-4≥0,
解得a≥2或a≤-2,
∴实数a的取值范围是(-∞,-2]∪[2,+∞).
点评 本题考查了对数函数的图象与性质的应用问题,也考查了不等式的恒成立问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.若曲线C1,y=x2与曲线C2:y=aex存在公切线,则a的( )
| A. | 最大值为$\frac{8}{{e}^{2}}$ | B. | 最大值为$\frac{4}{{e}^{2}}$ | C. | 最小值为$\frac{8}{{e}^{2}}$ | D. | 最小值为$\frac{4}{{e}^{2}}$ |
4.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,离心率e=$\frac{\sqrt{3}}{2}$,过原点的直线l交椭圆E于A,B两点,若|AF|+|BF|=4,则椭圆E的方程是( )
| A. | $\frac{{x}^{2}}{2}$+2y2=1 | B. | $\frac{{x}^{2}}{4}$+y2=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1 |
14.已知m∈R,函数f(x)=$\left\{\begin{array}{l}{|x+1|,}&{x<1}\\{lg(x-1),}&{x>1}\end{array}\right.$,g(x)=x2-2x+2m-2,若函数y=f(g(x))-m有6个零点,则实数m的取值范围是( )
| A. | (1,2) | B. | ($\frac{3}{4}$,1) | C. | ($\frac{2}{3}$,$\frac{3}{4}$) | D. | (0,$\frac{2}{3}$) |
18.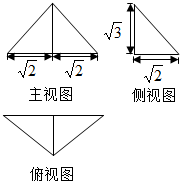 已知几何体的三视图如图所示,则该几何体的表面积为( )
已知几何体的三视图如图所示,则该几何体的表面积为( )
 已知几何体的三视图如图所示,则该几何体的表面积为( )
已知几何体的三视图如图所示,则该几何体的表面积为( )| A. | 4+$\sqrt{6}$ | B. | 6+$\sqrt{6}$ | C. | 2+2$\sqrt{2}$+$\sqrt{6}$ | D. | 2+2$\sqrt{3}$+$\sqrt{6}$ |
19.已知函数$f(x)=\left\{\begin{array}{l}{x^2}-1,x≤0\\ 3x,x>0\end{array}\right.$,若f(x)=15,则x=( )
| A. | 4或-4或5 | B. | 4或-4 | C. | -4或5 | D. | 4或5 |