题目内容
(19)如图,已知平行六面体ABCD—A1B
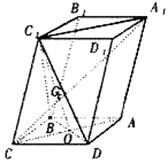
(Ⅰ)证明:C
(Ⅱ)当![]() 的值为多少时,能使A
的值为多少时,能使A
(19)本小题主要考查直线与直线、直线与平面的关系,逻辑推理能力。
(Ⅰ)证明:连结![]()
![]() 、
、![]() 和
和![]() 交于
交于![]() ,连结
,连结![]() 。
。
 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴![]() ⊥
⊥![]() ,
,![]() =
=![]() 。
。
又∵∠![]()
![]() =∠
=∠![]() ,
,![]() =
=![]() ,
,
∴![]() ,
,
∴![]() B=
B=![]() D,
D,
∵![]()
∴![]() ,
,
但![]() ,
,
∴![]() 平面
平面![]() 。
。
又![]() 平面
平面![]() ,
,
∴![]()
![]() 。
。
(Ⅱ)当![]() 时,能使
时,能使![]() 平面
平面![]() 。
。
证明一:
∵![]() ,
,
∴![]() ,又
,又![]() ,
,
由此可推得![]() 。
。
∴三棱锥![]() 是正三棱锥。
是正三棱锥。
设![]() 与
与![]() 相交于
相交于![]() 。
。
∵![]() ,且
,且![]() :
:![]() :1,
:1,
∴![]() :
:![]() =2:1。
=2:1。
又![]() 是正三角形
是正三角形![]() 的
的![]() 边上的高和中线,
边上的高和中线,
∴点![]() 是正三角形
是正三角形![]() 的中心,
的中心,
∴![]() 平面
平面![]() ,
,
即![]() 平面
平面![]() 。
。
证明:
由(Ⅰ)知,![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 。
。
当![]() 时,平行六面体的六个面是全等的菱形,
时,平行六面体的六个面是全等的菱形,
同![]() 的正法可得
的正法可得![]() 。
。
又![]() ,
,
∴![]() 平面
平面![]() 。
。

练习册系列答案
相关题目
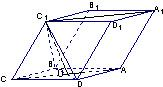
 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)
如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱) 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.