题目内容
下列命题中:
①若p?q,则?p??q;②命题“若A∩B=∅,则A=∅”的否命题;③若p:A⊆A∩B,q:A⊆A∪B,则p∨q为真;④函数f(x)=x2-3x+1,?x∈(0,1),f(x)=0.
其中真命题的个数是( )
①若p?q,则?p??q;②命题“若A∩B=∅,则A=∅”的否命题;③若p:A⊆A∩B,q:A⊆A∪B,则p∨q为真;④函数f(x)=x2-3x+1,?x∈(0,1),f(x)=0.
其中真命题的个数是( )
分析:根据互否命题真假性关系不确定,可判断①;写出原命题的否命题,根据集合交集的定义,可判断其真假;根据集合子集的定义及交集并集的运算法则,可判断③;根据零点存在定理可判断④.
解答:解:根据互否命题真假性关系不确定,可得当p?q时,?p??q不一定成立,故①为假命题;
命题“若A∩B=∅,则A=∅”的否命题为“若A∩B≠∅,则A≠∅”,当A∩B≠∅时,A,B有公共元素,则A一定有元素,故A≠∅,故②为真命题;
命题p:“A⊆A∩B”为假命题;但命题q:“A⊆A∪B”为真命题,故p∨q为真命题,故③为真命题;
函数f(x)=x2-3x+1为连续函数,且f(0)=1>0,f(1)=-1<0,即f(0)•f(1)<0,根据零点存在定理,可得?x∈(0,1),使f(x)=0,故④为真命题
故选B
命题“若A∩B=∅,则A=∅”的否命题为“若A∩B≠∅,则A≠∅”,当A∩B≠∅时,A,B有公共元素,则A一定有元素,故A≠∅,故②为真命题;
命题p:“A⊆A∩B”为假命题;但命题q:“A⊆A∪B”为真命题,故p∨q为真命题,故③为真命题;
函数f(x)=x2-3x+1为连续函数,且f(0)=1>0,f(1)=-1<0,即f(0)•f(1)<0,根据零点存在定理,可得?x∈(0,1),使f(x)=0,故④为真命题
故选B
点评:本题考查的知识点是四种命题,集合的运算法则及子集的定义,函数的零点存在性判断,难度不大,属于基础题.

练习册系列答案
相关题目
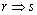 B.p:
B.p: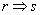 q:
q: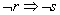
 q:
q:  D. p:
D. p: q:
q: