题目内容
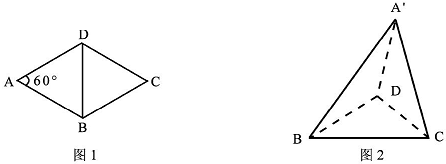（2013•凉山州二模）图1是边长为1的菱形，∠DAB=60°，现沿BD将△ABD翻折起，得四面体A′-BDC（图2），若二面角A′-BD-C的平面角为α（0＜a＜π），给出以下四个命题：①BD⊥A'C；
②A'C的长的范围是（0，
| 3 |
③当A'B⊥DC时，则cosα=
| 1 |
| 3 |
④当四面体A'-BDC体积最大时，A'-BDC的外接球的表面积是
| 5π |
| 3 |
其中真命题的个数为（ ）
分析：对于①取BD的中点E，连结A'E，EC，如图，则A'E⊥BD，EC⊥BD，利用线面垂直的判定得出BD⊥平面A'EC，从而得出①正确；②当α→0时，A'C→0，当α→π时，A'C→AC=
，从而得出A'C的长的范围；③当A'B⊥DC时，此时四面体A′-BDC是一个正四面体，设顶点A'在底面上的射影是Q，利用解直角三角形可求出二面角A′-BD-C的平面角的余弦值；④当四面体A'-BDC体积最大时，侧面A'BD⊥底面BCD，过底面BCD的中心Q作底面的垂线与侧面A'BD的中心作侧面A'BD的垂线的交点O即为A'-BDC的外接球的球心，利用直角三角形可得出A'-BDC的外接球的半径，从而得出答案．
| 3 |
解答：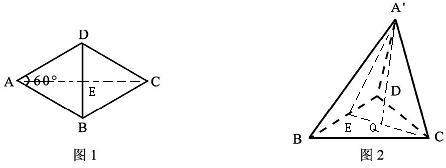
解：①取BD的中点E，连结A'E，EC，如图，则A'E⊥BD，EC⊥BD，∴BD⊥平面A'EC，A'C?平面A'EC，
∴BD⊥A'C；①正确；
②当α→0时，A'C→0，当α→π时，A'C→AC=
，
∴A'C的长的范围是（0，
）；正确；
③当A'B⊥DC时，此时四面体A′-BDC是一个正四面体，设顶点A'在底面上的射影是Q，则Q是三角形BCD的中心，
在直角三角形A'EQ中，则cosα=cos∠A′EC=
=
=
，
∴cosα=
；③正确；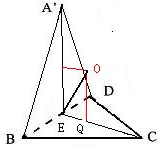
④当四面体A'-BDC体积最大时，侧面A'BD⊥底面BCD，如图，过底面BCD的中心Q作底面的垂线与侧面A'BD的中心作侧面A'BD的垂线的交点O即为A'-BDC的外接球的球心，
从而R2=OC2=OQ2+CQ2=(
×
)2+(
)2=
，
A'-BDC的外接球的表面积是4πR2=
．正确．
故选D．
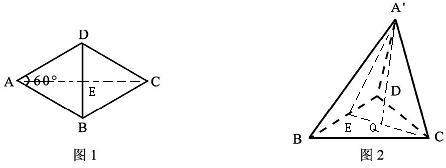解：①取BD的中点E，连结A'E，EC，如图，则A'E⊥BD，EC⊥BD，∴BD⊥平面A'EC，A'C?平面A'EC，∴BD⊥A'C；①正确；
②当α→0时，A'C→0，当α→π时，A'C→AC=
| 3 |
∴A'C的长的范围是（0，
| 3 |
③当A'B⊥DC时，此时四面体A′-BDC是一个正四面体，设顶点A'在底面上的射影是Q，则Q是三角形BCD的中心，
在直角三角形A'EQ中，则cosα=cos∠A′EC=
| EQ |
| A′E |
| EQ |
| CE |
| 1 |
| 3 |
∴cosα=
| 1 |
| 3 |
④当四面体A'-BDC体积最大时，侧面A'BD⊥底面BCD，如图，过底面BCD的中心Q作底面的垂线与侧面A'BD的中心作侧面A'BD的垂线的交点O即为A'-BDC的外接球的球心，
从而R2=OC2=OQ2+CQ2=(
| ||
| 2 |
| 1 |
| 3 |
| ||
| 3 |
| 5 |
| 12 |
A'-BDC的外接球的表面积是4πR2=
| 5π |
| 3 |
故选D．
点评：本题主要考查点到面的距离计算以及折叠问题．在解决折叠问题时，一定要注意分析出哪些量发生了变化，又有哪些量没有发生变化．
练习册系列答案
相关题目
（2013•凉山州二模）执行如图程序框图，输出结果是（ ）
（2013•凉山州二模）某几何体三视图如图所示，则其体积为（ ）