题目内容
(Ⅰ)设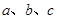 为正数,且
为正数,且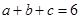 ,求证:
,求证: ;
;
(Ⅱ)设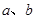 为正数,
为正数,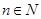 ,求证:
,求证: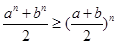
【答案】
(Ⅰ) 为正数,且
为正数,且 ,由柯西不等式有:
,由柯西不等式有:

 ,
,
当且仅当 ,即
,即 时等号成立,
时等号成立,
 .
……………6分
.
……………6分
(Ⅱ)证法一:用数学归纳法证明:
①当 时,左边
时,左边 =右边; 当
=右边; 当 时,左边
时,左边 =右边;
=右边;
当 时,左边
时,左边 右边,
右边,
所以当 时,不等式
时,不等式 成立;
成立;
②假设当 时不等式成立,即
时不等式成立,即 ,则当
,则当 时,
时,
 是正数,
是正数, ,
,

 ,
,  ,
,

所以当 时不等式也成立,
时不等式也成立,
综合①②得当 为正数,
为正数, 时,
时, 成立. ……………12分
成立. ……………12分
证法二:用构造法证明:
设 ,则:
,则: ,
,
 是正数
是正数 ,
,
 ,又
,又 ,
, ,
, ,
,
即当 为正数,
为正数, 时,
时, 成立.
成立.
【解析】略

练习册系列答案
相关题目
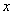 、
、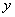 是不全为零的实数,试比较
是不全为零的实数,试比较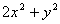 与
与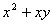 的大小;
的大小;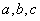 为正数,且
为正数,且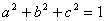 ,求证:
,求证: .
. 为正数,且
为正数,且 .求
.求 的最小值.
的最小值. 为正数,且
为正数,且 的最大值是 。
的最大值是 。