题目内容
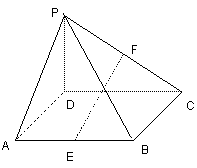
(满分14分) 如图,四棱锥P-ABCD中,底面ABCD
为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
求证:EF//平面PAD;
 若CD=2PD=2AD=2, 四棱锥P-ABCD外接球的表面积.
若CD=2PD=2AD=2, 四棱锥P-ABCD外接球的表面积.
(满分14分) 证明:(1)取PD的中点G,连接FG,GA,
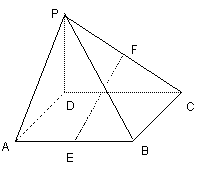 由G、F分别是PD、PC的中点,知GF是△PDC的中位线,
由G、F分别是PD、PC的中点,知GF是△PDC的中位线,
GF//DC,GF=![]() DC,---------------2分
DC,---------------2分
E是AB中点,AE=![]() AB,
AB,
矩形ABCD中,AB//DC,AB=DC,
∴GF//AE,GF=AE??---------------4分
∴四边形AEFG是平行四边形,EF//AG,---------------5分
EF在平面PDA外,AG在平面PDA内,
∴EF//平面PDA. ---------------7分
(2)由图易知AB⊥平面PAD,四棱锥P-ABCD的 外接球即以DP,DA,DC为棱的长方体的外接球。∴R=![]() ,∴S=4
,∴S=4![]() =6
=6![]() 。---------------14分
。---------------14分

练习册系列答案
相关题目
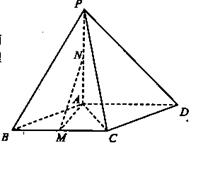

 平面
平面 ,
, ∥
∥ 是正三角形,且
是正三角形,且 .
.
 是线段
是线段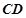 的中点,求证:
的中点,求证: ∥平面
∥平面 ;
;  与平面
与平面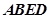 所成角的余弦值.
所成角的余弦值. 轴正半轴的交点,点B、P在单位圆上,且
轴正半轴的交点,点B、P在单位圆上,且 ,
,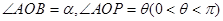 ,
, ,四边形OAQP的面积为S.
,四边形OAQP的面积为S. ;
; 的最大值及此时
的最大值及此时 的值
的值
 中,
中, ,点
,点 分别是
分别是 的中点.
求证:
的中点.
求证: 平面
平面 ;
; 平面
平面 .
.
 与曲线
与曲线 交于点O、A,直线
交于点O、A,直线 (0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。
(0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。
 ;
; 上的最大值。
上的最大值。