题目内容
从集合 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组 ,规定
,规定 .
.
(1)从所有的三元有序数组中任选一个,求它的所有元素之和等于10的概率
(2)定义三元有序数组 的“项标距离”为
的“项标距离”为 (其中
(其中 ),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
(1)0.2 (2)0.6
解析试题分析:解; (1)从集合 中任取三个不同元素构成三元有序数组如下
中任取三个不同元素构成三元有序数组如下









所有元素之和等于10的三元有序数组有

(2)项标距离为0的三元有序数组: , 项标距离为2的三元有序数组:
, 项标距离为2的三元有序数组:
项标距离为4的三元有序数组: , 项标距离为6的三元有序数组:
, 项标距离为6的三元有序数组:

考点:古典概型的概率
点评:主要是考查了古典概型概率的运用,属于基础题。

练习册系列答案
相关题目
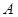 是函数
是函数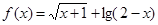 的定义域,集合
的定义域,集合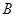 是函数
是函数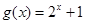 的值域.
的值域.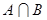 ;
;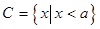 ,若集合
,若集合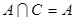 ,求实数
,求实数 的取值范围.
的取值范围.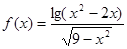 的定义域为
的定义域为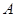 ,
,  ,且
,且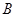 的真子集,求实数
的真子集,求实数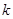 的取值范围.
的取值范围. ,其中
,其中 ,如果A∩B=B,求实数
,如果A∩B=B,求实数 的取值范围.
的取值范围. ,
, ,
, ,求
,求 ,
, ,
, ,
,
 ,
,
 ,求实数
,求实数 的值;
的值;  ,求实数
,求实数

 ;
; 的取值范围.
的取值范围.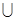 B;
B; },Q={1,m2+1,m+1}
},Q={1,m2+1,m+1} N;(2) 若M
N;(2) 若M Q,求实数m的值。
Q,求实数m的值。