Question

关于x的不等式x²-ax+2a＜0的解集为A，若集合A中恰有两个整数，则实数a的取值范围是________．

Answer 1

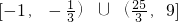
分析：由判别式△＞0，解得 a＜0，或 a＞8．①当a＜0时，由f（-1）＜0，且 f（-2）≥0，求得a的范围．②当a＞8时，由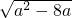≤3 求得8＜a≤9，再根据f（4）＜0，f（5）＜0，f（6）≥0求得a的范围．再把两个a的范围取并集，即得所求．
解答：由题意可得，判别式△=a²-8a＞0，解得 a＜0，或 a＞8．
①当a＜0时，由于f（0）＜0，且对称轴在y轴的左侧，故A中的两个整数为-1 和0，
设f（x）=x²-ax+2a，故有f（-1）=1+3a＜0，且 f（-2）=4+4a≥0．
解得-1≤a＜-．
②当a＞8时，对称轴x=＞4，设A=（m，n），则有n-m≤3，即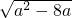≤3，
即a²-8a≤9，解得 8＜a≤9．
故有对称轴 4＜＜5，而f（2）=4＞0，f（3）=9-a≥0，
故A中的两个整数为4和5，故 f（4）＜0，f（5）＜0，f（6）≥0．
即 16-2a＜0，且25-3a＜0，36-4a≥0 解得 ＜a≤9．
综合可得，-1≤a＜-，或 ≤a≤9．
故实数a的取值范围是 ，
故答案为 ．
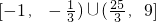点评：本题主要考查二次函数的性质，一元二次不等式的解法，属于基础题．