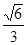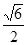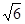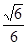题目内容
(本题满分15分)已知圆N: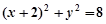 和抛物线C:
和抛物线C: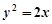 ,圆的切线
,圆的切线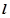 与抛物线C交于不同的两点A,B,
与抛物线C交于不同的两点A,B,
(1)当直线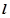 的斜率为1时,求线段AB的长;
的斜率为1时,求线段AB的长;
(2)设点M和点N关于直线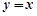 对称,问是否存在直线
对称,问是否存在直线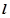 使得
使得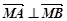 ?若存在,求出直线
?若存在,求出直线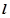 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
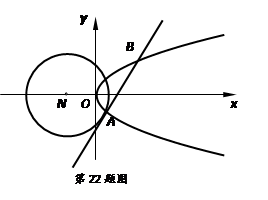
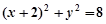 和抛物线C:
和抛物线C: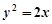 ,圆的切线
,圆的切线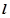 与抛物线C交于不同的两点A,B,
与抛物线C交于不同的两点A,B,(1)当直线
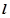 的斜率为1时,求线段AB的长;
的斜率为1时,求线段AB的长;(2)设点M和点N关于直线
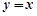 对称,问是否存在直线
对称,问是否存在直线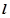 使得
使得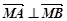 ?若存在,求出直线
?若存在,求出直线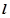 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.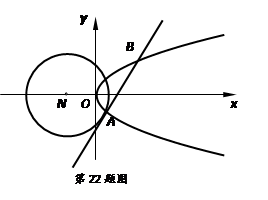
解:因为圆N: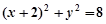 ,
,
所以圆心N为(-2,0),半径 , ………………… 1分
, ………………… 1分
设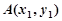 ,
,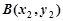 ,
,
(1)当直线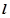 的斜率为1时,设
的斜率为1时,设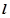 的方程为
的方程为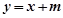 即
即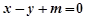
因为直线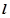 是圆N的切线,所以
是圆N的切线,所以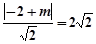 ,解得
,解得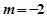 或
或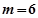 (舍)
(舍)
此时直线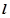 的方程为
的方程为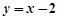 , ………………… 3分
, ………………… 3分
由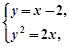 消去
消去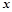 得
得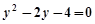 ,
,
所以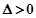 ,
,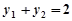 ,
,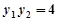 , ………………… 4分
, ………………… 4分
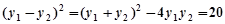
所以弦长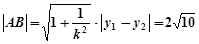 …………………6分
…………………6分
(2)①设直线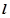 的方程为
的方程为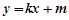 即
即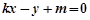 (
(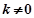 )
)
因为直线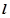 是圆N的切线,所以
是圆N的切线,所以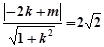 ,
,
得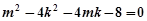 ………① ……………… 8分
………① ……………… 8分
由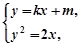 消去
消去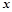 得
得 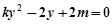 ,
,
所以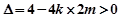 即
即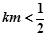 且
且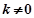 ,
,
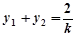 ,
,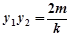 . ………………… 9分
. ………………… 9分
因为点M和点N关于直线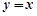 对称,所以点M为
对称,所以点M为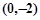
所以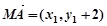 ,
,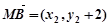 ,
,
因为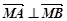 ,所以
,所以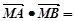
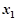
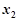 +
+ 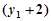
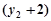
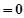 …… 10分
…… 10分
将A,B在直线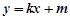 上代入化简得
上代入化简得
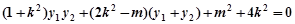 ……… 11分
……… 11分
代入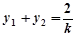 ,
,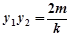 得
得
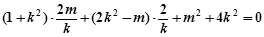
化简得 ………② ………… 12分
………② ………… 12分
①+②得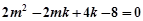
即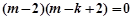 ,解得
,解得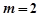 或
或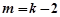
当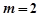 时,代入①解得
时,代入①解得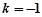 ,满足条件
,满足条件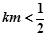 且
且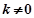 ,
,
此时直线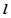 的方程为
的方程为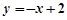 ;
;
当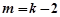 时,代入①整理得
时,代入①整理得 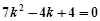 ,无解. …………… 13分
,无解. …………… 13分
② 当直线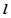 的斜率不存在时,
的斜率不存在时,
因为直线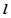 是圆N的切线,所以
是圆N的切线,所以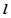 的方程为
的方程为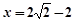 ,
,
则得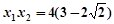 ,
,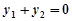 ,
,
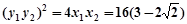 即
即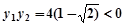
由①得: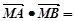
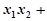
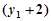
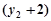
=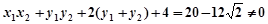
当直线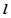 的斜率不存在时
的斜率不存在时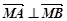 不成立. ……………… 14分
不成立. ……………… 14分
综上所述,存在满足条件的直线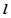 ,其方程为
,其方程为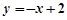 ……………… 15分
……………… 15分
另解:
(2)设直线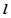 的方程为
的方程为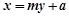 即
即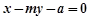 (
(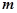 必存在)
必存在)
因为直线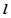 是圆N的切线,所以
是圆N的切线,所以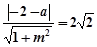 ,
,
得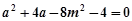 ………① ……………… 8分
………① ……………… 8分
由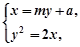 消去
消去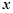 得
得 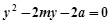 ,
,
所以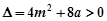 即
即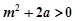 ………………… 9分
………………… 9分
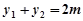 ,
,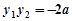 . ………………… 10分
. ………………… 10分
因为点M和点N关于直线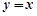 对称,所以点M为
对称,所以点M为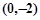
所以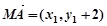 ,
,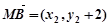 ,
,
因为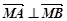 ,所以
,所以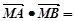
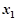
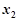 +
+ 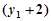
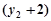
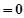 …… 11分
…… 11分
将A,B在直线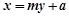 上代入化简得
上代入化简得
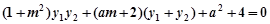 ……… 12分
……… 12分
代入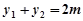 ,
,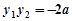 得
得
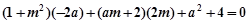
化简得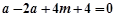 ………② ………… 13分
………② ………… 13分
①+②得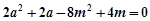
即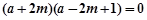 ,解得
,解得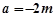 或
或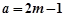 …… 14分
…… 14分
当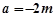 时,代入①解得
时,代入①解得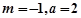 ,满足条件
,满足条件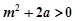 ;
;
当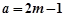 时,代入①整理得
时,代入①整理得 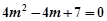 ,无解.
,无解.
综上所述,存在满足条件的直线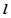 ,其方程为
,其方程为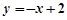 ……………… 15分
……………… 15分
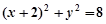 ,
,所以圆心N为(-2,0),半径
 , ………………… 1分
, ………………… 1分设
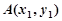 ,
,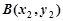 ,
,(1)当直线
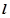 的斜率为1时,设
的斜率为1时,设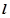 的方程为
的方程为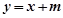 即
即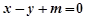
因为直线
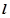 是圆N的切线,所以
是圆N的切线,所以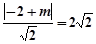 ,解得
,解得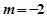 或
或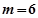 (舍)
(舍)此时直线
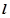 的方程为
的方程为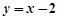 , ………………… 3分
, ………………… 3分由
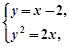 消去
消去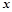 得
得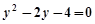 ,
,所以
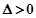 ,
,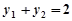 ,
,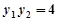 , ………………… 4分
, ………………… 4分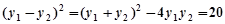
所以弦长
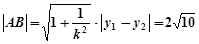 …………………6分
…………………6分(2)①设直线
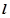 的方程为
的方程为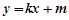 即
即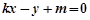 (
(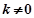 )
)因为直线
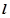 是圆N的切线,所以
是圆N的切线,所以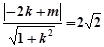 ,
,得
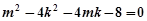 ………① ……………… 8分
………① ……………… 8分由
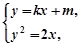 消去
消去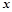 得
得 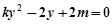 ,
,所以
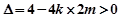 即
即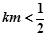 且
且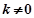 ,
, 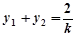 ,
,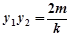 . ………………… 9分
. ………………… 9分因为点M和点N关于直线
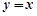 对称,所以点M为
对称,所以点M为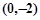
所以
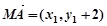 ,
,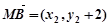 ,
, 因为
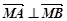 ,所以
,所以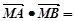
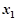
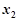 +
+ 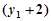
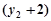
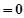 …… 10分
…… 10分将A,B在直线
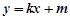 上代入化简得
上代入化简得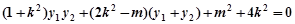 ……… 11分
……… 11分代入
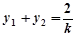 ,
,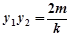 得
得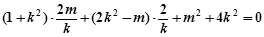
化简得
 ………② ………… 12分
………② ………… 12分①+②得
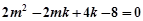
即
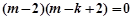 ,解得
,解得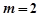 或
或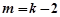
当
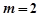 时,代入①解得
时,代入①解得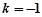 ,满足条件
,满足条件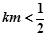 且
且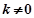 ,
,此时直线
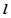 的方程为
的方程为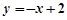 ;
;当
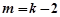 时,代入①整理得
时,代入①整理得 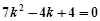 ,无解. …………… 13分
,无解. …………… 13分② 当直线
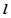 的斜率不存在时,
的斜率不存在时,因为直线
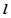 是圆N的切线,所以
是圆N的切线,所以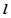 的方程为
的方程为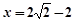 ,
,则得
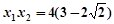 ,
,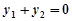 ,
,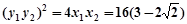 即
即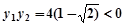
由①得:
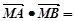
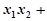
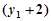
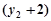
=
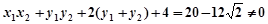
当直线
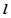 的斜率不存在时
的斜率不存在时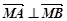 不成立. ……………… 14分
不成立. ……………… 14分综上所述,存在满足条件的直线
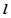 ,其方程为
,其方程为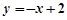 ……………… 15分
……………… 15分另解:
(2)设直线
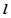 的方程为
的方程为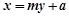 即
即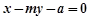 (
(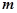 必存在)
必存在)因为直线
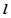 是圆N的切线,所以
是圆N的切线,所以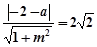 ,
,得
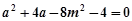 ………① ……………… 8分
………① ……………… 8分由
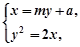 消去
消去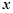 得
得 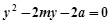 ,
,所以
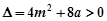 即
即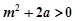 ………………… 9分
………………… 9分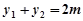 ,
,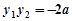 . ………………… 10分
. ………………… 10分因为点M和点N关于直线
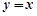 对称,所以点M为
对称,所以点M为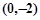
所以
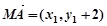 ,
,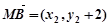 ,
, 因为
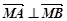 ,所以
,所以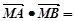
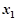
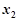 +
+ 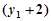
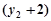
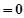 …… 11分
…… 11分将A,B在直线
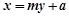 上代入化简得
上代入化简得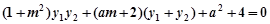 ……… 12分
……… 12分代入
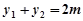 ,
,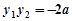 得
得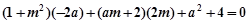
化简得
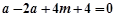 ………② ………… 13分
………② ………… 13分①+②得
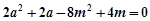
即
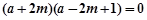 ,解得
,解得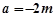 或
或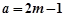 …… 14分
…… 14分当
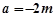 时,代入①解得
时,代入①解得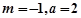 ,满足条件
,满足条件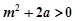 ;
;当
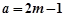 时,代入①整理得
时,代入①整理得 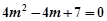 ,无解.
,无解.综上所述,存在满足条件的直线
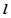 ,其方程为
,其方程为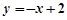 ……………… 15分
……………… 15分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
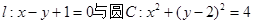 的位置关系是( )
的位置关系是( )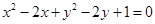 外一点
外一点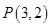 向这个圆作两条切线,则两切线夹角的正切值为( )
向这个圆作两条切线,则两切线夹角的正切值为( )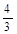
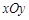 中,设直线
中,设直线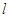 :
: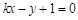 与圆
与圆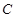 :
: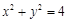 相交于
相交于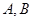 两点,以
两点,以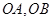 为邻边作平行四边形
为邻边作平行四边形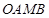 ,若点
,若点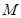 在圆
在圆 。
。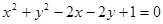 相切的直线
相切的直线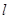 交x轴、y轴于A、B两点,O为原点,|OA|=3,|OB|=b(b>2).
交x轴、y轴于A、B两点,O为原点,|OA|=3,|OB|=b(b>2).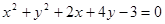 上到直线x+y+1=0的距离为
上到直线x+y+1=0的距离为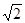 的点有( )
的点有( )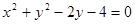 ,直线
,直线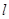 :mx-y+1-m=0
:mx-y+1-m=0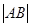 =3
=3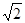 ,求直线
,求直线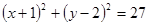 与
与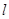 :
: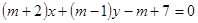 ,
,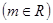
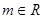 ,
, 此时
此时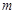 的值。
的值。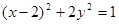 上,则
上,则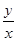 的最大值为( )
的最大值为( )