题目内容
已知函数![]() 和函数
和函数![]() ,其中
,其中![]() 为参数,且满足
为参数,且满足![]() .
.
(1)若![]() ,写出函数
,写出函数![]() 的单调区间(无需证明);
的单调区间(无需证明);
(2)若方程![]() 在
在![]() 恒有唯一解,求实数
恒有唯一解,求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
解:(1)m=2时,g(x)=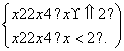 …………………………………………………1分
…………………………………………………1分
函数g(x)的单调增区间为(-∞,1),(2,+∞),单调减区间为(1,2). ……………4分
(2)由f(x)=2|m|在x∈[-4,+∞)恒有唯一解,
得|x-m|=|m|在x∈[-4,+∞)恒有唯一解.
即![]() ,解得
,解得![]() 或
或![]() ,由题意知2m=0或2m<-4,
,由题意知2m=0或2m<-4,
即m<-2或m=0.
综上,m的取值范围是m<-2或m=0.……………………………………………………8分
(3)f(x)=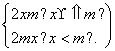
则f(x)的值域应是g(x)的值域的子集.………………………………………………………10分
①m≤4时,f(x)在(-∞,m]上单调递减,[m,4]上单调递增,故f(x)≥f(m)=1.
g(x)在[4,+∞)上单调递增,故g(x)≥g(4)=8-2m,所以8-2m≤1,
即![]() ≤m≤4. ………………………………………………………………………………12分
≤m≤4. ………………………………………………………………………………12分
②当4<m≤8时,f(x)在(-∞,4]上单调递减,故f(x)≥f(4)=2m-4,
g(x)在[4,m]上单调递减,[m,+∞)上单调递增,故g(x)≥g(m)=2m-8,
所以2m-4≥2m-8,解得4<m≤5或6≤m≤8. …………………………………13分
综上,m的取值范围是![]() . ……………………………………………………14分
. ……………………………………………………14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
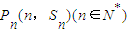 均在函数y=f(x)的图象上.
均在函数y=f(x)的图象上. ,其中n∈N*,求{nbn}的前n项和.
,其中n∈N*,求{nbn}的前n项和.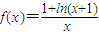 和g(x)=x-1-ln(x+1)
和g(x)=x-1-ln(x+1)