题目内容
设f(x)=px-
-2lnx.
(Ⅰ)若f(x)在其定义域内为单调递增函数,求实数p的取值范围;
(Ⅱ)设g(x)=
,且p>0,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围.
| p |
| x |
(Ⅰ)若f(x)在其定义域内为单调递增函数,求实数p的取值范围;
(Ⅱ)设g(x)=
| 2e |
| x |
分析:(I)由 f(x)=px-
-2lnx,得f′(x)=p+
-
=
.由px2-2x+p≥0在(0,+∞)内恒成立,能求出P的范围.
(II)法1:g(x)=
在[1,e]上是减函数,所以g(x)∈[2,2e].原命题等价于[f(x)]max>[g(x)]min=2,x∈[1,e],由[f(x) ]max=f(e)=p(e-
) -2lne>2,解得p>
,由此能求出p的取值范围.
法2:原命题等价于f(x)-g(x)>0在[1,e)上有解,设F(x)=f(x)-g(x)=px-
-2lnx-
,由F′(x)=p+
-
+
=
>0,知F(x)是增函数,由[F(x)]max=F(e)>0,能求出p的取值范围.
| p |
| x |
| p |
| x2 |
| 2 |
| x |
| px2-2x+p |
| x2 |
(II)法1:g(x)=
| 2e |
| x |
| 1 |
| e |
| 4e |
| e2-1 |
法2:原命题等价于f(x)-g(x)>0在[1,e)上有解,设F(x)=f(x)-g(x)=px-
| p |
| x |
| 2e |
| x |
| p |
| x2 |
| 2 |
| x |
| 2e |
| x2 |
=
| px2+p+2(e-x) |
| x2 |
解答:解:(I)由 f(x)=px-
-2lnx,
得f′(x)=p+
-
=
.…(3分)
要使f(x)在其定义域(0,+∞)内为单调增函数,只需f′(x)≥0,
即px2-2x+p≥0在(0,+∞)内恒成立,…(5分)
从而P≥1.…(7分)
(II)解法1:g(x)=
在[1,e]上是减函数,
所以[g(x)]min=g(e)=2,[g(x)]max=g(1)=2e,即g(x)∈[2,2e].
当0<p<1时,由x∈[1,e],得x-
≥ 0,
故f(x)=p(x-
)-2lnx<x-
-2lnx<2,不合题意.…(10分)
当P≥1时,由(I)知f(x)在[1,e]连续递增,f(1)=0<2,又g(x)在[1,e]上是减函数,
∴原命题等价于[f(x)]max>[g(x)]min=2,x∈[1,e],…(12分)
由[f(x) ]max=f(e)=p(e-
) -2lne>2,解得p>
,
综上,p的取值范围是(
,+∞).…(15分)
解法2:原命题等价于f(x)-g(x)>0在[1,e)上有解,
设F(x)=f(x)-g(x)=px-
-2lnx-
,
∵F′(x)=p+
-
+
=
>0,
∴F(x)是增函数,…(10分)
∴[F(x)]max=F(e)>0,解得p>
,
∴p的取值范围是(
,+∞).…(15分)
| p |
| x |
得f′(x)=p+
| p |
| x2 |
| 2 |
| x |
| px2-2x+p |
| x2 |
要使f(x)在其定义域(0,+∞)内为单调增函数,只需f′(x)≥0,
即px2-2x+p≥0在(0,+∞)内恒成立,…(5分)
从而P≥1.…(7分)
(II)解法1:g(x)=
| 2e |
| x |
所以[g(x)]min=g(e)=2,[g(x)]max=g(1)=2e,即g(x)∈[2,2e].
当0<p<1时,由x∈[1,e],得x-
| 1 |
| x |
故f(x)=p(x-
| 1 |
| x |
| 1 |
| x |
当P≥1时,由(I)知f(x)在[1,e]连续递增,f(1)=0<2,又g(x)在[1,e]上是减函数,
∴原命题等价于[f(x)]max>[g(x)]min=2,x∈[1,e],…(12分)
由[f(x) ]max=f(e)=p(e-
| 1 |
| e |
| 4e |
| e2-1 |
综上,p的取值范围是(
| 4e |
| e2-1 |
解法2:原命题等价于f(x)-g(x)>0在[1,e)上有解,
设F(x)=f(x)-g(x)=px-
| p |
| x |
| 2e |
| x |
∵F′(x)=p+
| p |
| x2 |
| 2 |
| x |
| 2e |
| x2 |
=
| px2+p+2(e-x) |
| x2 |
∴F(x)是增函数,…(10分)
∴[F(x)]max=F(e)>0,解得p>
| 4e |
| e2-1 |
∴p的取值范围是(
| 4e |
| e2-1 |
点评:本题考查得用导数求函数最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 -2lnx.
-2lnx.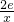 ,且p>0,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围.
,且p>0,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围. -2lnx.
-2lnx. ,且p>0,若在[1,e]上至少存在一点x,使得f(x)>g(x)成立,求实数p的取值范围.
,且p>0,若在[1,e]上至少存在一点x,使得f(x)>g(x)成立,求实数p的取值范围. -2lnx.
-2lnx. ,且p>0,若在[1,e]上至少存在一点x,使得f(x)>g(x)成立,求实数p的取值范围.
,且p>0,若在[1,e]上至少存在一点x,使得f(x)>g(x)成立,求实数p的取值范围. -2lnx.
-2lnx. ,且p>0,若在[1,e]上至少存在一点x,使得f(x)>g(x)成立,求实数p的取值范围.
,且p>0,若在[1,e]上至少存在一点x,使得f(x)>g(x)成立,求实数p的取值范围.