Question

已知定义在R上的函数f（x）=asinωx+bcosωx（ω＞0）的周期为π，且对一切x∈R，都有f（x）；

（1）求函数f（x）的表达式； 

（2）若g（x）=f（），求函数g（x）的单调增区间．

Answer 1

考点：

三角函数中的恒等变换应用；两角和与差的正弦函数；二倍角的正弦．

专题：

计算题．

分析：

（1）利用辅助角公式化简，通过周期求出ω，通过函数的最值，列出方程，求出函数的解析式即可．

（2）利用g（x）=f（）求出函数的解析式，利用正弦函数的单调性，求出函数的单调区间即可．

解答：

解：（1）∵，又周期

∴ω=2

∵对一切x∈R，都有f（x）

∴

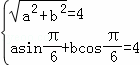
得：

∴f（x）的解析式为

（2）∵，

∴g（x）的增区间是函数y=sin的减区间

∴由得g（x）的增区间为（k∈Z）

（等价于）．

点评：

本题考查三角函数中的恒等变换应用，两角和与差的正弦函数，二倍角的正弦，考查计算能力．