Question

已知二次函数f(x)=ax²+(a²+b)x+c的图象开口向上，且f(0)=1，f(1)=0，则实数b的取值范围是(    )

A.（-∞,-]                            B.［-,0)

C.［0,+∞)                              D.(-∞,-1)

Answer 1

思路解析：依题意得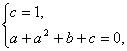

整理,得a²+a+b+1=0，解得a=，

∵图象开口向上，∴a＞0.

∴a=＞0.

解得b＜-1.

∵二次函数f(x)=ax²+(a²+b)x+c的图象过点（0，1）和点（1，0），

又∵图象开口向上，

∴点（0，1）必须在抛物线对称轴的左侧，即抛物线的对称轴在点（0，1）的右侧，即y轴的右侧.

∴x=-＞0.

∴a²+b＜0.当b＜-1时，a²+b＜0恒成立.∴b＜-1.因此，选D.

答案：D