题目内容
(本小题满分14分)已知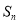 是数列
是数列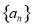 的前
的前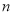 项和,且满足
项和,且满足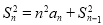 (
(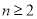 ,
,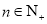 ),又已知
),又已知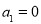 ,
,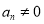 ,
, ,
,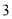 ,
,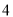 ,
, .
.
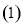 计算
计算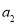 ,
,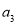 ,并求数列
,并求数列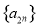 的通项公式;
的通项公式;
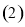 若
若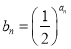 ,
,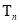 为数列
为数列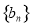 的前
的前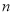 项和,求证:
项和,求证: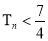 .
.
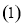
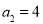


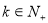 (2)
(2)
【解析】
试题分析:(1)由题意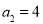 ,
,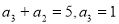 ,由
,由 可求数列
可求数列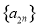 的通项公式
的通项公式
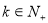
(2)由(1)可得
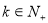 所以对于数列
所以对于数列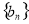 的前
的前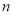 项和
项和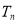 有
有
①当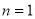 时,
时,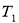 =
=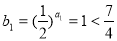
②当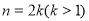 时:
时:
③当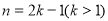 时:四种情况讨论可得
时:四种情况讨论可得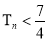
试题解析:、(1)当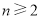 时,由已知得
时,由已知得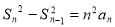
因为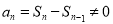 ,所以
,所以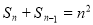 …… ①
…… ①
当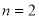 时,
时,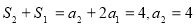
又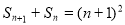 ……②
……②
由②-①得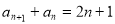 . …… ③
. …… ③
当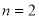 时,
时,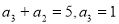
对于③式又有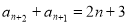 . …… ④
. …… ④
由④-③得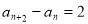 (
(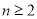 ) …… ⑤
) …… ⑤
⑤表明:数列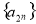 是以
是以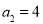 为首项,2为公差的等差数列,
为首项,2为公差的等差数列,
所以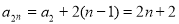 ,
,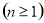
又因为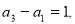 不满足⑤
不满足⑤
而⑤也表明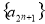 是从
是从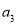 开始,以2为公差的等差数列,
开始,以2为公差的等差数列,
所以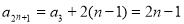 ,
,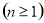
所以 ,
,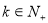
(2)由(1)可得
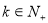
所以对于数列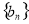 的前
的前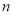 项和
项和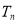 有
有
①当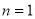 时,
时,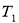 =
=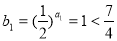
②当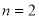 时
时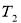 =
=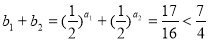
③当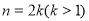 时,
时,
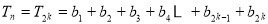
=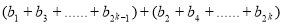
=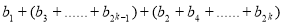
=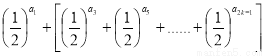
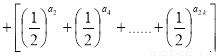


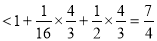
④当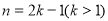 时,
时,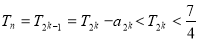
综上所述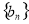 的前
的前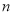 项和
项和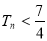 对任意正整数成立)
对任意正整数成立)
考点:数列的通项公式,数列的前n项和的求法
考点分析: 考点1:数列的综合应用 考点2:数列的求和 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 为虚数单位,复数
为虚数单位,复数
 的虚部
的虚部 记作
记作
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 的等边
的等边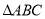 中,
中,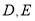 分别在边BC与AC上,且
分别在边BC与AC上,且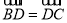 ,
,
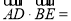 ( )
( )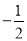 B.
B. 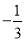 C.
C.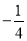 D.
D.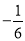
 为等差数列,
为等差数列, ,
, ,则
,则 .
.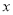 与
与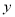 正相关,且由观测数据算得样本平均数
正相关,且由观测数据算得样本平均数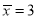 ,
,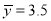 ,则由该观测数据算得的线性回归方程可能是( )
,则由该观测数据算得的线性回归方程可能是( )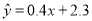 B.
B.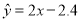 C.
C.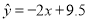 D.
D.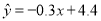
 是
是 的高,
的高, 是
是 外接圆的直径,若
外接圆的直径,若 ,则
,则 .
.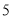 天的日平均温度均不低于
天的日平均温度均不低于
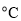 ”.现有甲、乙、丙三地连续
”.现有甲、乙、丙三地连续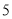 天的日平均温度的记录数据(记录数据都是正整数):
天的日平均温度的记录数据(记录数据都是正整数):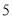 个数据的中位数为
个数据的中位数为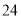 ,众数为
,众数为 ;
;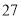 ,总体均值为
,总体均值为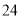 ;
; ,总体均值为
,总体均值为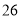 ,总体方差为
,总体方差为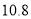 .
. 有两个极值点,则实数
有两个极值点,则实数 的取值范围是 .
的取值范围是 . 为圆
为圆 的切线,
的切线, 为切点,
为切点,
 ,
,
 的角平分线与
的角平分线与 和圆
和圆 和
和 .
.

 的值.
的值.