题目内容
设函数f（x）=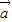
-
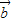，其中向量
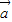=（m，cos2x），
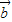=（1+sin2x，1），x∈R，且函数y=f（x）的图象经过点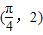
（Ⅰ）求实数m的值；
（Ⅱ）求函数f（x）的最小值及此时x的取值集合．
【答案】分析：（Ⅰ）由向量的数量积的坐标表示可得，f（x）=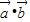
=m（1+sin2x）+cos2x=m+msin2x+cos2x，由f（
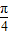）=2可求m
（Ⅱ）由（Ⅰ）得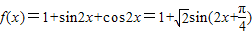
，结合正弦函数的性质可求
解答：解：（Ⅰ）∵f（x）=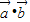
=m（1+sin2x）+cos2x=m+msin2x+cos2x
由已知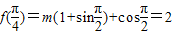
，
∴2m=2即m=1
（Ⅱ）由（Ⅰ）得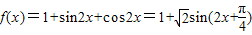
∴当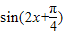
=-1时，f（x）的最小值为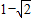
此时2x+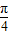
=
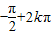即{x|
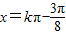，k∈Z}
点评：本题主要考查了向量的数量积的坐标表示，辅助角公式在三角函数化简中的应用，正弦函数的性质的应用，属于基础试题
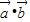=m（1+sin2x）+cos2x=m+msin2x+cos2x，由f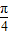（）=2可求m（Ⅱ）由（Ⅰ）得
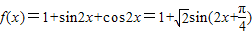，结合正弦函数的性质可求解答：解：（Ⅰ）∵f（x）=
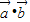=m（1+sin2x）+cos2x=m+msin2x+cos2x由已知
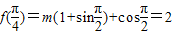，∴2m=2即m=1
（Ⅱ）由（Ⅰ）得
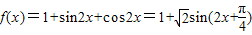
∴当
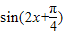=-1时，f（x）的最小值为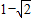此时2x+
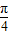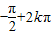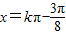=即{x|，k∈Z}点评：本题主要考查了向量的数量积的坐标表示，辅助角公式在三角函数化简中的应用，正弦函数的性质的应用，属于基础试题
练习册系列答案
相关题目
（2012•重庆）设函数f（x）在R上可导，其导函数为f′（x），且函数y=（1-x）f′（x）的图象如图所示，则下列结论中一定成立的是（ ）