题目内容
在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE,且BC=1,则点A到平面BCD的距离为 .
【答案】分析:利用等边三角形的性质可得BO,DF.利用中线长定理可得DE,再利用勾股定理可得DF2=DE2+EF2,
AO2=AB2-BO2,即可得出.
解答:解:如图所示,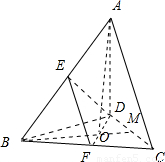 作AO⊥平面BCD,则点O为底面BCD的中心.
作AO⊥平面BCD,则点O为底面BCD的中心.
∵△BCD是边长为1的等边三角形,
∴BO=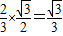 ,
,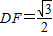 .
.
设AB=2x,利用中线长定理可得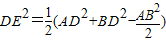 =
=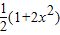 .
.
∵EF⊥DE,∴EF2+DE2=DF2.
∵EF=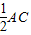 =x,∴
=x,∴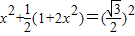 ,化为
,化为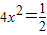 .
.
∵AO⊥平面BCD,∴AO⊥BO.
∴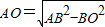 =
=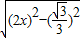 =
=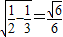 .
.
故答案为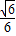 .
.
点评:熟练掌握等边三角形的性质、中线长定理、中位线定理、勾股定理等是解题的关键.
AO2=AB2-BO2,即可得出.
解答:解:如图所示,
 作AO⊥平面BCD,则点O为底面BCD的中心.
作AO⊥平面BCD,则点O为底面BCD的中心.∵△BCD是边长为1的等边三角形,
∴BO=
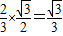 ,
,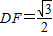 .
.设AB=2x,利用中线长定理可得
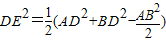 =
=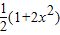 .
.∵EF⊥DE,∴EF2+DE2=DF2.
∵EF=
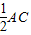 =x,∴
=x,∴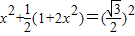 ,化为
,化为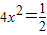 .
.∵AO⊥平面BCD,∴AO⊥BO.
∴
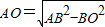 =
=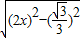 =
=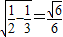 .
.故答案为
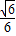 .
.点评:熟练掌握等边三角形的性质、中线长定理、中位线定理、勾股定理等是解题的关键.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 如图,在正三棱锥A-BCD中,底面正三角形BCD的边长为2,点E是AB的中点,AC⊥DE,则正三棱锥A-BCD的体积是
如图,在正三棱锥A-BCD中,底面正三角形BCD的边长为2,点E是AB的中点,AC⊥DE,则正三棱锥A-BCD的体积是 如图所示,在正三棱锥A-BCD中,E,F分别为BD,AD的中点,EF⊥CF,则直线BD与平面ACD所成的角为
如图所示,在正三棱锥A-BCD中,E,F分别为BD,AD的中点,EF⊥CF,则直线BD与平面ACD所成的角为