题目内容
已知函数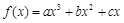 (
(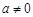 )是定义在
)是定义在 上的奇函数,且
上的奇函数,且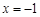 时,函数
时,函数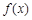 取极值1.
取极值1.
(Ⅰ)求函数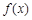 的解析式;
的解析式;
(Ⅱ)令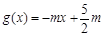 ,若
,若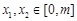 (
(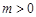 ),不等式
),不等式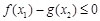 恒成立,求实数
恒成立,求实数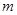 的取值范围;
的取值范围;
【答案】
(Ⅰ)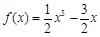 (Ⅱ)
(Ⅱ)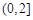
【解析】
试题分析:(Ⅰ)函数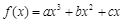 (
(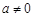 )是定义在R上的奇函数,
)是定义在R上的奇函数,
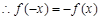 恒成立,即
恒成立,即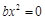 对于
对于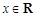 恒成立,
恒成立,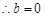 .
2分
.
2分
则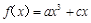 ,
,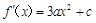 ,
,
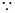
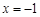 时,函数取极值1.∴
时,函数取极值1.∴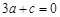 ,
,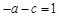 ,
,
解得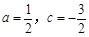 .∴
.∴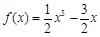 .
4分
.
4分
(Ⅱ)不等式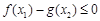 恒成立,只需
恒成立,只需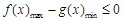 即可.
5分
即可.
5分
∵函数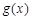 在
在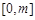 上单调递减,∴
上单调递减,∴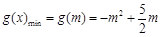 .
6分
.
6分
又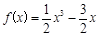 ,
,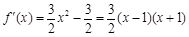 ,
,
由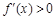 得
得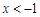 或
或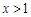 ;
;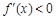 得
得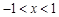 ,
,
故函数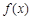 在
在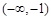 ,
,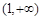 上单调递增,在
上单调递增,在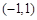 上单调递减,
上单调递减,
则当 时,
时,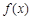 取得极小值,
8分
取得极小值,
8分
在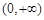 上,当
上,当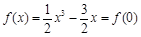 时,
时,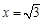 ,
,
①当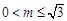 时,
时,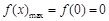 ,
,
则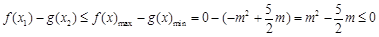 ,
,
解得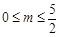 ,故此时
,故此时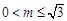 .
10分
.
10分
②当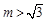 时,
时,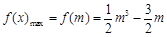 ,
,
则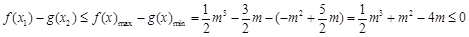 ,
,
解得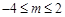 ,故此时
,故此时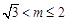 .综上所述,实数m的取值范围是
.综上所述,实数m的取值范围是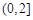 . 12分
. 12分
考点:函数奇偶性极值最值
点评:第一问中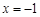 时,函数
时,函数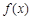 取极值1中隐含了两个关系式:
取极值1中隐含了两个关系式: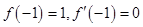 ;,第二问不等式恒成立问题求参数范围的,常转化为求函数最值问题,本题中要注意的是
;,第二问不等式恒成立问题求参数范围的,常转化为求函数最值问题,本题中要注意的是 的取值范围是不同的,因此应分别求两函数最值
的取值范围是不同的,因此应分别求两函数最值

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
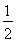
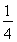
 C.-
C.- 或-
或-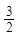 ,0)时,f(x)=log2(-3x+1),则f(2011)=( )
,0)时,f(x)=log2(-3x+1),则f(2011)=( )