题目内容
函数y＝x的单调递减区间为( )
| A．(－∞，1) | B．(－∞，0) |
| C．[0，＋∞) | D．(－∞，＋∞) |
B
解析
练习册系列答案
相关题目
设函数
，若
时，
＞0恒成立，则实数m的取值范围是（ ）
| A．（0，1） | B．（-∞，0） | C．（-∞，） | D．（-∞，1） |
已知函数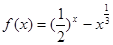
，那么在下列区间中含有函数
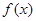零点的是
A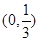． | B． |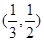
C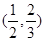． | D． |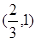
用
表示
两数中的最小值，若函数
的图象关于直线
对称，则t的值为 （ ）
| A．—2 | B．2 |
| C．—1 | D．1 |
已知偶函数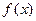
在区间
单调增加，则满足
的
的取值范围是 
（ ）
A． | B． | C．  | D． |
函数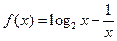
的零点所在区间为
A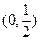． | B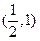． | C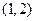． | D． |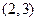
某商场对顾客实行购物优惠活动，规定一次购物付款总额：①如果不超过200元，则不予优惠，②如果超过200元但不超过500元，则按标价给予9折优惠，③如果超过500元，其500元按②条给予优惠，超过500元的部分给予7折优惠．某人两次去购物，分别付款168元和423元，假设他一次购买上述同样的商品，则应付款( )
| A．413.7元 | B．513.7元 | C．546.6元 | D．548.7元 |
已知函数f(x)＝logax(a>0，a≠1)的图象，如下图所示，函数y＝g(x)的图象与y＝f(x)的图象关于直线y＝x对称，则函数y＝g(x)的解析式为( )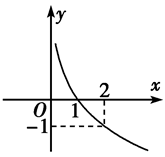
| A．g(x)＝2x | B．g(x)＝x |
| C．g(x)＝logx | D．g(x)＝log2x |
函数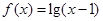
的定义域是
A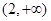． | B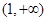． | C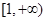． | D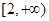． |