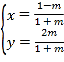题目内容
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点下的距离为10.
到其焦点下的距离为10.
(1)求抛物线C的方程;
(2)设过焦点F的的直线![]() 与抛物线C交于
与抛物线C交于![]() 两点,且抛物线在
两点,且抛物线在![]() 两点处的切线分别交x轴于
两点处的切线分别交x轴于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)由抛物线的定义,可得到![]() ,即可求出
,即可求出![]() ,从而得到抛物线的方程;(Ⅱ)直线
,从而得到抛物线的方程;(Ⅱ)直线![]() 的斜率一定存在,可设斜率为
的斜率一定存在,可设斜率为![]() ,直线
,直线![]() 为
为![]() ,设
,设![]() ,
,![]() ,由
,由![]() 可得
可得![]() ,
,![]() ,
,![]() ,然后对
,然后对![]() 求导,可得到
求导,可得到![]() 的斜率及方程表达式,进而可表示出
的斜率及方程表达式,进而可表示出![]() ,同理可得到
,同理可得到![]() 的表达式,然后对
的表达式,然后对![]() 化简可求出范围。
化简可求出范围。
解:(Ⅰ)已知![]() 到焦点
到焦点![]() 的距离为10,则点
的距离为10,则点![]() 到准线的距离为10.
到准线的距离为10.
∵抛物线的准线为![]() ,∴
,∴![]() ,
,
解得![]() ,∴抛物线的方程为
,∴抛物线的方程为![]() .
.
(Ⅱ)由已知可判断直线![]() 的斜率存在,设斜率为
的斜率存在,设斜率为![]() ,因为
,因为![]() ,则
,则![]() :
:![]() .
.
设![]() ,
,![]() ,由
,由![]() 消去
消去![]() 得,
得,![]() ,
,
∴![]() ,
,![]() .
.
由于抛物线![]() 也是函数
也是函数![]() 的图象,且
的图象,且![]() ,则
,则![]() :
:![]() .
.
令![]() ,解得
,解得![]() ,∴
,∴![]() ,从而
,从而![]() .
.
同理可得,![]() ,
,
∴![]()
![]()
![]() .
.
∵![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目