题目内容
(2012•唐山二模)向圆(x一2)2+(y-
)2=4内随机掷一点,则该点落在x轴下方的概率为
-
-
.
| 3 |
| 1 |
| 6 |
| ||
| 4π |
| 1 |
| 6 |
| ||
| 4π |
分析:确定该点落在x轴下方的部分为一弓形,其面积等于一圆心角为60°的扇形减去一等边三角形的面积,利用圆的面积为4π,即可求得该点落在x轴下方的概率.
解答:解:由题意,设圆心为C,圆与x轴的交点为A,B,则∠ACB=60°
该点落在x轴下方的部分为一弓形,其面积等于一圆心角为60°的扇形减去一等边三角形的面积.
∴弓形的面积为
-
∵圆的面积为4π
∴该点落在x轴下方的概率为
=
-
故答案为:
-
该点落在x轴下方的部分为一弓形,其面积等于一圆心角为60°的扇形减去一等边三角形的面积.
∴弓形的面积为
| 2π |
| 3 |
| 3 |
∵圆的面积为4π
∴该点落在x轴下方的概率为
| ||||
| 4π |
| 1 |
| 6 |
| ||
| 4π |
故答案为:
| 1 |
| 6 |
| ||
| 4π |
点评:本题考查几何概型,解题的关键是确定该点落在x轴下方的部分的面积.

练习册系列答案
相关题目
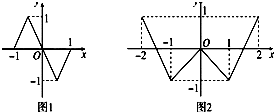 (2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )
(2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )