题目内容
方程x2+x-1=xex2-1+(x2-1)ex的解集为A(x∈R)则A中所有元素的平方和等于( )
分析:先观察、变形、估测方程的实数根,然后通过分类讨论加以证明即可.
解答:解:将方程x2+x-l=xex2-1+(x2-1)ex变为x2-1=x(ex2-1-1)+(x2-1)ex,可知x=±1,0时满足方程,
∴x=±1,0是方程的解.
下面证明此方程的解只有±1,0.
证明:①当x>1时,把方程变为x×
+ex-1=0,
∵x>1,∴ex2-1>1,x2-1>0,ex-1>e-1>0,故左边>0,即方程没有大于1的解;
②当x<-1时,把方程变为1-x×
=ex,
∵x<-1,∴ex2-1>1,x2-1>0,故左边>1,而右边=ex<e-1=
<1,∴左边≠右边,即方程没有小于-1的解;
③当0<x<1时,把方程变为x×
+ex-1=0,
∵0<x<1,∴ex2-1<1,x2-1<0,ex>1,∴左边>0,即方程没有大于0而小于1的解;
④当-1<x<0时,把方程变为1-x×
=ex,
∵-1<x<0,∴ex2-1<1,x2-1<0,ex<1,∴左边>1,右边<1,即方程没有大-1而小于0的解.
综上可知:此方程只有±1,0三个实数根.
∴A={-1,1,0}.
∴则A中所有元素的平方和=12+(-1)2+0=2.
故答案为C.
∴x=±1,0是方程的解.
下面证明此方程的解只有±1,0.
证明:①当x>1时,把方程变为x×
| ex2-1-1 |
| x2-1 |
∵x>1,∴ex2-1>1,x2-1>0,ex-1>e-1>0,故左边>0,即方程没有大于1的解;
②当x<-1时,把方程变为1-x×
| ex2-1-1 |
| x2-1 |
∵x<-1,∴ex2-1>1,x2-1>0,故左边>1,而右边=ex<e-1=
| 1 |
| e |
③当0<x<1时,把方程变为x×
| ex2-1-1 |
| x2-1 |
∵0<x<1,∴ex2-1<1,x2-1<0,ex>1,∴左边>0,即方程没有大于0而小于1的解;
④当-1<x<0时,把方程变为1-x×
| ex2-1-1 |
| x2-1 |
∵-1<x<0,∴ex2-1<1,x2-1<0,ex<1,∴左边>1,右边<1,即方程没有大-1而小于0的解.
综上可知:此方程只有±1,0三个实数根.
∴A={-1,1,0}.
∴则A中所有元素的平方和=12+(-1)2+0=2.
故答案为C.
点评:本题培养学生的观察、变形、估测能力,同时注意分类讨论的思想应用.本题较好的培养了学生的灵活解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤. ,其中α,β是方程x2-x-1=0的两个根.
,其中α,β是方程x2-x-1=0的两个根.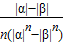 ,n=1,2,…,证明:
,n=1,2,…,证明: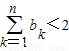 .
.