题目内容
已知数列{an}满足a1=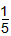 ,且有an-1-an-4an-1an=0,(n≥2,n∈N*)。
,且有an-1-an-4an-1an=0,(n≥2,n∈N*)。
(1)求证:数列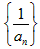 为等差数列;
为等差数列;
(2)试问a1a2是否是数列{an}中的项?如果是, 是第几项;如果不是,请说明理由。
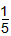 ,且有an-1-an-4an-1an=0,(n≥2,n∈N*)。
,且有an-1-an-4an-1an=0,(n≥2,n∈N*)。(1)求证:数列
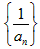 为等差数列;
为等差数列; (2)试问a1a2是否是数列{an}中的项?如果是, 是第几项;如果不是,请说明理由。
解:(1)∵an-1-an-4an-1an=0(n≥2,n∈N*),
∴两边同除以an-1an得 (n≥2,n∈N*),
(n≥2,n∈N*),
∴数列 是以
是以 为首项,4为公差的等差数列;
为首项,4为公差的等差数列;
(2)由(1)得
∴ ,
,
∴
设a1a2是数列 中的第t项,则
中的第t项,则 ,解得t=11
,解得t=11
∴a1a2是数列 中的第11项。
中的第11项。

练习册系列答案
相关题目