题目内容
A是定义在[2,4]上且满足如下条件的函数φ(x)组成的集合:
①对任意的x∈[1,2],都有φ(2x)∈(1,2);
②存在常数L(0<L<1),使得对任意的x1,x2∈[1,2],都有|φ(2x1)-φ(2x2)|≤L|x1-x2|.
(Ⅰ)设φ(2x)=![]() ,x∈[2,4],证明:φ(x)∈A
,x∈[2,4],证明:φ(x)∈A
(Ⅱ)设φ(x)∈A,如果存在x0∈(1,2),使得x0=φ(2x0),那么这样的x0是唯一的;
(Ⅲ)设φ(x)∈A,任取x1∈(1,2),令xn-1=φ(2xn),n=1,2,…,证明:给定正整数k,对任意的正整数p,成立不等式|xk+p-xk|≤![]() |x2-x1|
|x2-x1|
答案:

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
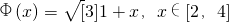 ,证明:Φ(x)∈A;
,证明:Φ(x)∈A;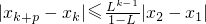 成立.
成立. ,证明:Φ(x)∈A;
,证明:Φ(x)∈A; 成立.
成立. ,证明:Φ(x)∈A;
,证明:Φ(x)∈A; 成立.
成立.