题目内容
在正方体AC1中,M、N分别为棱AA1和BB1的中点,若θ为CM与D1N所成的角,则sinθ的值为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
D
解法一:以D为原点建立空间直角坐标系:
设正方体棱长为1,则:D(0,0,0),M(1,0,![]() ),
),
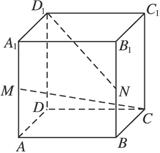
C(0,1,0),N(1,1,![]() ),D1(0,0,1).
),D1(0,0,1).
![]() =(1,-1,
=(1,-1,![]() ),
),![]() =(1,1,-
=(1,1,-![]() ),
),
![]() ·
·![]() =1-1-
=1-1-![]() =-
=-![]() ,|
,|![]() |=
|=![]() =
=![]() ,|
,|![]() |=
|=![]() =
=![]() ,
,
∴cos<![]() ,
, ![]() >
>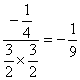 .sin<
.sin<![]() ,
,![]() >=
>=![]() .
.
解法二:取D1D的中点为E.
连结ME、MB、EC,则四边形BMEC为矩形.连结BE,则MC、BE是矩形BMEC的对角线,
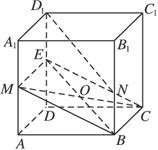
又BN![]() D1E
D1E![]()
![]() BB1,
BB1,
∴四边形BND1E是平行四边形.
∴D1N![]() BE,则BE与CM所成的角就是D1N与CM所成的角.
BE,则BE与CM所成的角就是D1N与CM所成的角.
设MC与BE交于O,正方体和棱长为2,则MC=BE=D1N=3.
OE=OM=![]() .
.
在△MOE中,
cosMOE=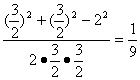 ·sin∠MOE=
·sin∠MOE=![]() .
.
即∠MOE是CM与D1M所成的角θ,
∴sinθ=![]() .
.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
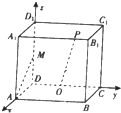 如图所示,在正方体AC1中,M是棱DD1的中点,O是平面ABCD的中心,P是A1B1上的任意一点,则直线AM与OP所成角是
如图所示,在正方体AC1中,M是棱DD1的中点,O是平面ABCD的中心,P是A1B1上的任意一点,则直线AM与OP所成角是