题目内容
如下图所示，已知
AB为⊙O的直径，AC为弦，OD∥BC，交AC于D，BC=4cm，(1)试判断OD与AC的关系；(2)求OD的长；(3)若2sinA－1=0，求⊙O的直径．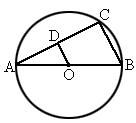
答案：垂直；2cm;8cm
解析：
提示：
解析：
|
解： (1)OD⊥AC，理由：∵AB为⊙O的直径，∴∠ACB=90°．∵OD∥BC(如上图)，∴∠ADO=∠ACB=90°，∴OD⊥AC．(2) ∵△AOD∽△ABC，∴ ，∴ ．
(3) ∵2sinA－1=0，∴ ，∴ ，∵ ，
∴ AB=2BC=8cm． |
提示：
|
分析：由直径条件可知，∠ACB=90°，O是AB的中点，这样利用OD∥BC可得OD⊥AC，用相似可得OD长，由边角关系可求⊙O的直径． |
练习册系列答案
相关题目
平面PBC＝l．
AB；
+
+
=0．
