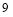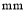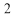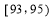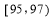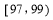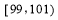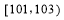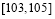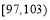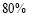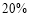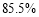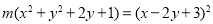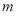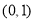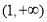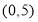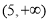题目内容
已知常数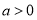 ,向量
,向量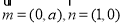 ,经过定点
,经过定点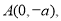 以
以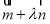 为方向向量的直线与经过定点
为方向向量的直线与经过定点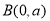 以
以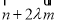 为方向向量的直线相交于
为方向向量的直线相交于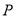 ,其中
,其中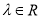 ,
,
(1)求点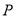 的轨迹
的轨迹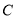 的方程;(2)若
的方程;(2)若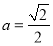 ,过
,过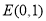 的直线交曲线
的直线交曲线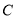 于
于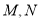 两点,求
两点,求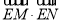 的取值范围。
的取值范围。
(I) ;(II)
;(II)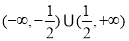
【解析】
试题分析:(I)利用向量共线定理和坐标运算即可得出;
(II)对直线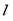 的斜率分类讨论,当直线
的斜率分类讨论,当直线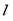 的斜率存在时,设直线
的斜率存在时,设直线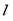 的方程为y=kx+1与双曲线的方程联立,即可得到根与系数的关系,再利用向量的数量积和对k分类讨论即可得出.
的方程为y=kx+1与双曲线的方程联立,即可得到根与系数的关系,再利用向量的数量积和对k分类讨论即可得出.
试题解析:(1)设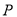 点的坐标为
点的坐标为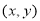 ,则
,则
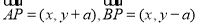 ,
,
又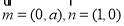 ,
,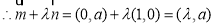 ,
,
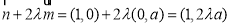 ,
,
又因为向量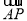 与向量
与向量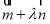 平行,所以
平行,所以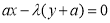
向量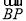 与向量
与向量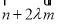 平行,所以
平行,所以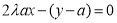 ,两式联立消去
,两式联立消去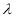 得
得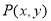 的轨迹方程为
的轨迹方程为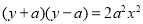 ,即
,即 。
。
(2)因为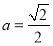 ,所以
,所以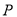 的轨迹
的轨迹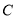 的方程为
的方程为 ,
,
此时点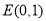 为双曲线的焦点。
为双曲线的焦点。
(I)若直线的斜率不存在,其方程为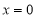 ,
,
与双曲线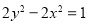 的两焦点为
的两焦点为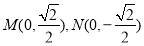 ,
,
此时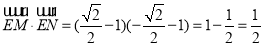
(II)若直线的斜率存在,设其方程为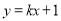 ,
,
由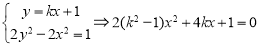 ,设交点为
,设交点为
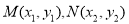 ,则
,则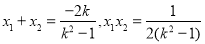 ,
,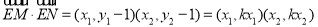
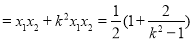
当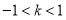 时,
时,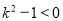 ,
,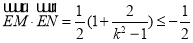 ;
;
当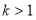 或
或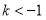 时,
时, ,
,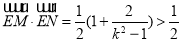 ;
;
综上可知,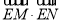 的取值范围是
的取值范围是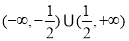 。
。
考点:(1)圆锥曲线的综合应用;(2)向量在解析几何中的应用.

练习册系列答案
相关题目