题目内容
(本小题满分12分)
如图,平面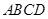 ⊥平面
⊥平面 ,
, 是直角三角形,
是直角三角形,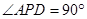 ,四边形
,四边形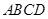 是直角梯形,其中
是直角梯形,其中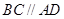 ,
,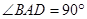 ,
,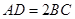 ,且
,且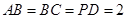 ,
,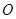 是
是 的中点,
的中点,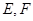 分别是
分别是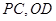 的中点.
的中点.

(Ⅰ)求证: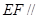 平面
平面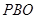 ;
;
(Ⅱ)求二面角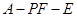 的正切值.
的正切值.
【答案】
(Ⅰ)取 的中点
的中点 ,证明四边形
,证明四边形 为平行四边形, ∴
为平行四边形, ∴ ,则
,则 平面
平面 (Ⅱ)2
(Ⅱ)2
【解析】
试题分析:(Ⅰ)取 的中点
的中点 ,连接
,连接 ,由
,由 为
为 中点,
中点,
故

 又
又 为
为 中点,∴
中点,∴
 ,
,
∴

 ,故四边形
,故四边形 为平行四边形,
……3分
为平行四边形,
……3分
∴ ,则
,则 平面
平面 .
……4分
.
……4分
(Ⅱ) 连接 ,则
,则 ,又
,又 ,平面
,平面 ⊥平面
⊥平面 ,
,
∴ ⊥面
⊥面 , 故面
, 故面 ⊥面
⊥面 ,
……6分
,
……6分
过 作
作 于
于 ,则
,则 ⊥面
⊥面 ,
,
过 作
作 于
于 ,连
,连 ,
,
则 ,故
,故 为二面角
为二面角 的平面角,
……8分
的平面角,
……8分
由于 为
为 的中点,故
的中点,故 =
=
 =
=
 =1,
=1,
∵ ,
, ,
,
由 为
为 的中点,故
的中点,故 ,又
,又 为
为 的中点,可知
的中点,可知 ,
,
从而 ,又
,又 是
是 的中点,∴
的中点,∴ 为
为 的中点∴
的中点∴ =
=
 =
= , ……11分
, ……11分
∴ =
= =2,∴二面角
=2,∴二面角 平面角的正切值为2.
……12分
平面角的正切值为2.
……12分
考点:本小题主要考查空间中线面平行的证明和二面角的求解,考查学生的空间想象能力和运算求解能力.
点评:证明空间中直线、平面间的位置关系时,要紧扣判定定理和性质定理,定理中要求的条件缺一不可.

练习册系列答案
相关题目