题目内容
函数f（x）在定义域R内可导，若f（x）=f（2-x），且当x∈（-∞，1）时，（x-1）•f′（x）＜0，a=f（0），b=f（
），c=f（3），则（ ）
| 1 |
| 2 |
分析：由题意可得，函数f（x）的图象关于直线x=1对称，在（-∞，1）上是增函数，再根据c=f（-1），
＞0＞-1，利用函数的单调性判断a、b、c的大小关系．
| 1 |
| 2 |
解答：解：由f（x）=f（2-x）可得函数f（x）的图象关于直线x=1对称，
当x∈（-∞，1）时，（x-1）•f′（x）＜0，∴函数f（x）在（-∞，1）上是增函数，在（1，+∞）上是减函数，
由于c=f（3）=f（2-3）=f（-1），
＞0＞-1，a=f（0），b=f（
），c=f（3），∴b＞a＞c，
故选C．
当x∈（-∞，1）时，（x-1）•f′（x）＜0，∴函数f（x）在（-∞，1）上是增函数，在（1，+∞）上是减函数，
由于c=f（3）=f（2-3）=f（-1），
| 1 |
| 2 |
| 1 |
| 2 |
故选C．
点评：本题主要考查函数的图象的对称性和单调性的应用，体现了转化的数学思想，属于中档题．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
已知函数f(x)=
，令g(x)=f(
)．
（1）求函数f（x）的值域；
（2）任取定义域内的5个自变量，根据要求计算并填表；观察表中数据间的关系，猜想一个等式并给予证明；
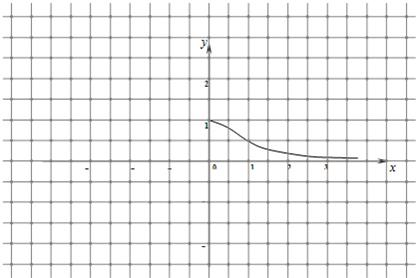
（3）如图，已知f（x）在区间[0，+∞）的图象，请据此在该坐标系中补全函数f（x）在定义域内的图象，并在同一坐标系中作出函数g（x）的图象．请说明你的作图依据．
| 1 |
| x2+1 |
| 1 |
| x |
（1）求函数f（x）的值域；
（2）任取定义域内的5个自变量，根据要求计算并填表；观察表中数据间的关系，猜想一个等式并给予证明；
| x | … | |||||||
f(x)-
|
… | |||||||
g(x)-
|
… |