题目内容
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点.则异面直线EF与BD所成角的余弦值为( )
A.

B.

C.

D.

【答案】分析:欲求异面直线EF与BD所成的角的大小,只需平移两条异面直线中的一条,使它们成为相交直线,则相交直线所成的锐角或直角,就是异面直线所成角,再放入三角形中,通过解三角形,求出此角.
解答:解:取BC的中点M,连接EM、FM,则FM∥BD,

∴∠EFM(或其补角)就是异面直线EF与BD所成的角.
∵平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,
∴EM= =
= ,EF=
,EF= ,
,
又FM= BD=
BD= ,
,
∴在△MFE中,cos∠EFM= =
= ,
,
∴异面直线EF与BD所成角的余弦值为
故选D.
点评:本题考查异面直线所成角的求法,考查学生的计算能力,属于基础题.
解答:解:取BC的中点M,连接EM、FM,则FM∥BD,

∴∠EFM(或其补角)就是异面直线EF与BD所成的角.
∵平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,
∴EM=
 =
= ,EF=
,EF= ,
,又FM=
 BD=
BD= ,
,∴在△MFE中,cos∠EFM=
 =
= ,
,∴异面直线EF与BD所成角的余弦值为

故选D.
点评:本题考查异面直线所成角的求法,考查学生的计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.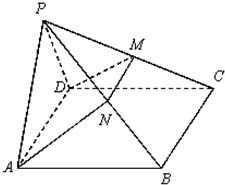 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.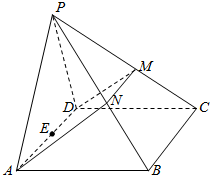 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.