题目内容
已知 其中
其中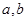 为常数,若
为常数,若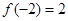 ,则
,则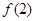 =( )
=( )
| A.2 | B.-6 | C.-10 | D.-4 |
C
解析试题分析:根据题意可知,∵f(-2)=-8a-2b-4=2,∴8a+2b=-6,∴f(2)=8a+2b-4=-10,故答案为C。也可以利用整体的思想来分析得到f(2)+f(-2)=-8,进而得到结论,选C.
考点:本试题主要考查了函数奇偶性的运用,利用整体思想求解函数的值,属于基础试题
点评:解决该试题的关键是能构造函数f(x)+4=g(x),分析可知g(x)是一个奇函数,那么则有g(-x)+g(x)=0.进而求解得到。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设f(x)是R上的奇函数,且当x>0时,f(x)=x(1+ ),则当x<0时,f(x)=( )
),则当x<0时,f(x)=( )
A.-x(1+ ) ) | B.x(1+ ) ) | C.-x(1- ) ) | D. x(1- ) ) |
已知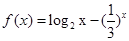 ,若实数
,若实数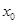 是方程
是方程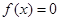 的解,且
的解,且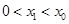 ,则
,则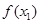 的值是( )
的值是( )
| A.恒为负 | B.等于零 | C.恒为正 | D.不小于零 |
设函数 上单调递增,则
上单调递增,则 的大小关系为( )
的大小关系为( )
A. | B. |
C. | D.不确定 |
已知函数 在区间
在区间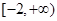 上是增函数,则
上是增函数,则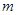 的范围是
的范围是
A.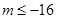 | B. | C.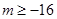 | D.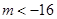 |
设f(x)是R上的奇函数.当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=
| A.1 | B.3 | C.-1 | D.-3 |
下列四个函数,不在区间[1,2]上单调递减的是
A.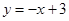 | B.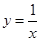 | C.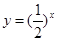 | D.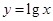 |
下列各组表示同一函数的是( )
A.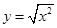 与 与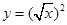 | B.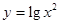 与 与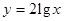 |
C.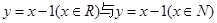 | D.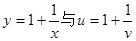 |
已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 是偶函数,当
是偶函数,当 时,
时, ,则
,则 =【 】
=【 】
| A.8 | B.- | C. | D.-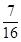 |