题目内容
已知函数 是奇函数,且f(1)=2
是奇函数,且f(1)=2(1)求f(x)的表达式;
(2)
 ,记
,记 ,求S的值.
,求S的值.
【答案】分析:(1)由f(x)为奇函数,得其定义域为为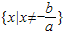 ,∴
,∴ ,又f(1)=2,得
,又f(1)=2,得 ,联立即可求得a,b的值;
,联立即可求得a,b的值;
(2)先求等式F(a)+F 及F(1)的值,由此规律即可求得S.
及F(1)的值,由此规律即可求得S.
解答:解:(1)∵ 是奇函数,∴a≠0,其定义域为
是奇函数,∴a≠0,其定义域为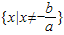 ,
,
∴ ①,又f(1)=2,得
①,又f(1)=2,得 ②,由①②解得b=0,a=1,
②,由①②解得b=0,a=1,
∴ .
.
(2) (x>0),
(x>0),
 ,
,
而 ,
,
所以S=F(1)+F(2)+F(3)+…+F(2012)+F( )+F(
)+F( )+…+F(
)+…+F( )=F(1)+2011=
)=F(1)+2011= .
.
点评:本题考查函数解析式的求法及奇函数的性质,考查学生分析问题解决问题的能力.
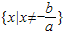 ,∴
,∴ ,又f(1)=2,得
,又f(1)=2,得 ,联立即可求得a,b的值;
,联立即可求得a,b的值;(2)先求等式F(a)+F
 及F(1)的值,由此规律即可求得S.
及F(1)的值,由此规律即可求得S.解答:解:(1)∵
 是奇函数,∴a≠0,其定义域为
是奇函数,∴a≠0,其定义域为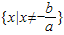 ,
,∴
 ①,又f(1)=2,得
①,又f(1)=2,得 ②,由①②解得b=0,a=1,
②,由①②解得b=0,a=1,∴
 .
.(2)
 (x>0),
(x>0), ,
,而
 ,
,所以S=F(1)+F(2)+F(3)+…+F(2012)+F(
 )+F(
)+F( )+…+F(
)+…+F( )=F(1)+2011=
)=F(1)+2011= .
.点评:本题考查函数解析式的求法及奇函数的性质,考查学生分析问题解决问题的能力.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目

 是奇函数,且
是奇函数,且
 ,
, 的值;
的值; 在区间
在区间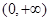 上是减函数.
上是减函数.  是奇函数,且在区间
是奇函数,且在区间 上单调递减,则
上单调递减,则 上是( )
上是( )  B. 单调递减函数,且有最大值
B. 单调递减函数,且有最大值 D.
单调递增函数,且有最大值
D.
单调递增函数,且有最大值 是奇函数,且
是奇函数,且 .
. 上的单调性,并加以证明.
上的单调性,并加以证明.  是奇函数,且图像在点
是奇函数,且图像在点
 为自然对数的底数)处的切线斜率为3.
为自然对数的底数)处的切线斜率为3. 、
、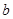 的值;
的值; ,且
,且 对任意
对任意 恒成立,求
恒成立,求 的最大值;
的最大值; 时,证明:
时,证明:
 是奇函数,且满足
是奇函数,且满足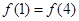
 、
、 的值;
的值;
 在区间
在区间 单调递减,在区间
单调递减,在区间 单调递增;
单调递增; 同时满足以下两个条件:1不等式
同时满足以下两个条件:1不等式 对
对 恒成立;
2方程
恒成立;
2方程 在
在 上有解.若存在,试求出实数
上有解.若存在,试求出实数