题目内容
已知函数f(x)=asinxcosx+ acos2x-
acos2x- a+1(a>0)的定义域为R,当
a+1(a>0)的定义域为R,当 时,f(x)的最大值为2
时,f(x)的最大值为2
(1)求a的值
(2)用五点法作出该函数在长度为一个周期的闭区间上的图象
(3)写出该函数的单调递增区间及对称中心的坐标.
解:(1)f(x)=asinxcosx+ acos2x-
acos2x- a+1
a+1
=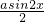 +
+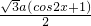 -
- +1
+1
=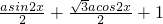
=a(sin2xcos +cos2xsin
+cos2xsin )+1
)+1
=asin(2x+ )+1
)+1
当 ,则
,则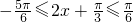
∴当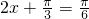 ,f(x)有最大值为
,f(x)有最大值为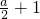 ,
,
又∵f(x)的最大值为2,∴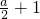 =2,
=2,
解得:a=2.
(2)由(1)知
令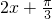 分别取0,
分别取0, ,π,
,π, ,2π,则对应的x与y的值如下表
,2π,则对应的x与y的值如下表
画出函数在区间[- ,
, ]的图象如下图
]的图象如下图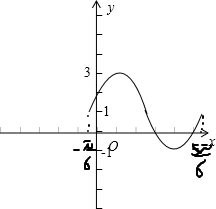
(2)
令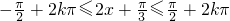 ,k∈Z
,k∈Z
解得,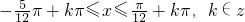
∴函数的增区间为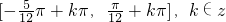 .
.
令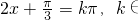 Z,解得x=
Z,解得x= ,k∈Z,
,k∈Z,
∴函数 的对称中心的横坐标为
的对称中心的横坐标为 ,k∈Z,
,k∈Z,
又∵函数 的图象是函数
的图象是函数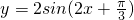 的图象向上平移一个单位长度得到的,
的图象向上平移一个单位长度得到的,
∴函数 的对称中心的纵坐标为1.
的对称中心的纵坐标为1.
∴对称中心坐标为( ,1)k∈Z
,1)k∈Z
分析:(1)先利用二倍角公式和辅助角公式把函数f(x)化为y=Asin(ωx+φ)+h的形式,利用正弦函数的性质求出最大值,又因为已知函数的最大值为2,就可求出参数a的值.
(2)利用“五点法”作图,令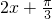 分别取0,
分别取0, ,π,
,π, ,2π,求出对应的x与y的值,就可得到函数在一个周期内的五个关键点的坐标,画出见图.
,2π,求出对应的x与y的值,就可得到函数在一个周期内的五个关键点的坐标,画出见图.
(3)令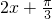 属于正弦函数的增区间,解出x的范围即为函数f(x)的单调增区间.
属于正弦函数的增区间,解出x的范围即为函数f(x)的单调增区间.
令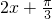 =kπ,k∈Z,解得x的值为函数对称中心的横坐标,因为函数
=kπ,k∈Z,解得x的值为函数对称中心的横坐标,因为函数 的图象是函数
的图象是函数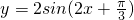 的图象向上平移一个单位长度得到的,所以函数
的图象向上平移一个单位长度得到的,所以函数 的对称中心的纵坐标为1.就可得到函数
的对称中心的纵坐标为1.就可得到函数 的对称中心.
的对称中心.
点评:本题主要考查应用三角函数的公式把三角函数化简为y=Asin(ωx+φ)+h的形式,再求图象与性质,属于三角函数的综合题.
 acos2x-
acos2x- a+1
a+1=
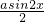 +
+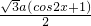 -
- +1
+1=
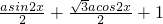
=a(sin2xcos
 +cos2xsin
+cos2xsin )+1
)+1=asin(2x+
 )+1
)+1当
 ,则
,则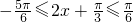
∴当
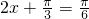 ,f(x)有最大值为
,f(x)有最大值为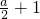 ,
,又∵f(x)的最大值为2,∴
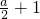 =2,
=2,解得:a=2.
(2)由(1)知

令
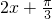 分别取0,
分别取0, ,π,
,π, ,2π,则对应的x与y的值如下表
,2π,则对应的x与y的值如下表| x | - |  |  |  |  |
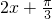 | 0 |  | π |  | 2π |
| y | 1 | 3 | -1 | 1 | 3 |
 ,
, ]的图象如下图
]的图象如下图
(2)

令
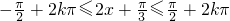 ,k∈Z
,k∈Z解得,
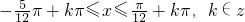
∴函数的增区间为
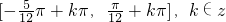 .
.令
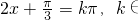 Z,解得x=
Z,解得x= ,k∈Z,
,k∈Z,∴函数
 的对称中心的横坐标为
的对称中心的横坐标为 ,k∈Z,
,k∈Z,又∵函数
 的图象是函数
的图象是函数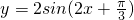 的图象向上平移一个单位长度得到的,
的图象向上平移一个单位长度得到的,∴函数
 的对称中心的纵坐标为1.
的对称中心的纵坐标为1.∴对称中心坐标为(
 ,1)k∈Z
,1)k∈Z分析:(1)先利用二倍角公式和辅助角公式把函数f(x)化为y=Asin(ωx+φ)+h的形式,利用正弦函数的性质求出最大值,又因为已知函数的最大值为2,就可求出参数a的值.
(2)利用“五点法”作图,令
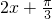 分别取0,
分别取0, ,π,
,π, ,2π,求出对应的x与y的值,就可得到函数在一个周期内的五个关键点的坐标,画出见图.
,2π,求出对应的x与y的值,就可得到函数在一个周期内的五个关键点的坐标,画出见图.(3)令
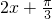 属于正弦函数的增区间,解出x的范围即为函数f(x)的单调增区间.
属于正弦函数的增区间,解出x的范围即为函数f(x)的单调增区间.令
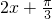 =kπ,k∈Z,解得x的值为函数对称中心的横坐标,因为函数
=kπ,k∈Z,解得x的值为函数对称中心的横坐标,因为函数 的图象是函数
的图象是函数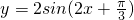 的图象向上平移一个单位长度得到的,所以函数
的图象向上平移一个单位长度得到的,所以函数 的对称中心的纵坐标为1.就可得到函数
的对称中心的纵坐标为1.就可得到函数 的对称中心.
的对称中心.点评:本题主要考查应用三角函数的公式把三角函数化简为y=Asin(ωx+φ)+h的形式,再求图象与性质,属于三角函数的综合题.

练习册系列答案
相关题目