题目内容
椭圆![]() 的长轴长为
的长轴长为![]() ,且
,且![]() 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)过椭圆右焦点的直线![]() 交椭圆于
交椭圆于![]() 两点,若以
两点,若以![]() 为直径的圆过原点,求直线
为直径的圆过原点,求直线![]() 方程.
方程.
解:(Ⅰ)由题意:![]() ,
,![]() .所求椭圆方程为
.所求椭圆方程为![]() .
.
又点![]() 在椭圆上,可得
在椭圆上,可得![]() .所求椭圆方程为
.所求椭圆方程为![]() . …5分
. …5分
(Ⅱ)由(Ⅰ)知![]() ,所以
,所以![]() ,椭圆右焦点为
,椭圆右焦点为![]() .
.
因为以![]() 为直径的圆过原点,所以
为直径的圆过原点,所以![]() .
.
若直线![]() 的斜率不存在,则直线
的斜率不存在,则直线![]() 的方程为
的方程为![]() .
.
直线![]() 交椭圆于
交椭圆于![]() 两点,
两点, ![]() ,不合题意.
,不合题意.
若直线![]() 的斜率存在,设斜率为
的斜率存在,设斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
由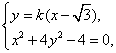 可得
可得![]() .
.
由于直线![]() 过椭圆右焦点,可知
过椭圆右焦点,可知![]() .
.
设![]() ,则
,则![]() ,
,
![]() .
.
所以![]() .
.
由![]() ,即
,即![]() ,可得
,可得![]() .
.
所以直线![]() 方程为
方程为![]() .………………14分
.………………14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的长轴长为
的长轴长为 ,且点
,且点 在椭圆上.
在椭圆上. 交椭圆于
交椭圆于 两点,若以
两点,若以 为直径的圆过原点,
为直径的圆过原点, 的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线
的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线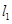 过点
过点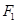 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线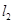 垂直
垂直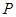 ,线段
,线段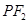 垂直平分线交
垂直平分线交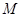
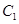 的标准方程和动点
的标准方程和动点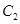 的方程。
的方程。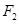 作斜率为1的直线交椭圆于A、B两点,求
作斜率为1的直线交椭圆于A、B两点,求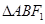 的面积。
的面积。 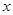 轴交于点
轴交于点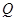 ,不同的两点
,不同的两点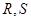 在轨迹
在轨迹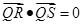 求证:直线
求证:直线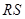 恒过
恒过