题目内容
20.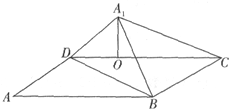 如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.
如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.(Ⅰ)求证:BC⊥A1D;
(Ⅱ)求证:平面A1CD⊥平面A1BC;
(Ⅲ)若AB=10,BC=6,求三棱锥A1-BCD的体积.
分析 ((I)证明BC⊥A1O.推出BC⊥平面A1CD.通过直线与平面垂直的性质定理证明BC⊥A1D.
(II)证明A1D⊥A1B.推出A1D⊥平面A1BC.然后证明平面A1BC⊥平面A1CD.
(III)利用${V}_{{A}_{1}-BCD}={V}_{D-{A}_{1}BC}$,求出底面面积与高,即可求出几何体的体积.
解答 (共14分)
解:(I)因为A1在平面BCD上的射影O在CD上,
所以A1O⊥平面BCD.
又BC?平面BCD,
所以BC⊥A1O.
又BC⊥CO,CO∩A1O=O,CO?平面A1CD,A1O?平面A1CD,
所以BC⊥平面A1CD.
又A1D?平面A1CD,
所以BC⊥A1D.(5分)
(II)因为矩形ABCD,
所以A1D⊥A1B.
由(I)知BC⊥A1D.
又BC∩A1B=B,BC?平面A1BC,A1B?平面A1BC,
所以A1D⊥平面A1BC.
又A1D?平面A1CD,
所以平面A1BC⊥平面A1CD.(10分)
(III)因为A1D⊥平面A1BC,
所以A1D⊥A1C.
因为CD=10,A1D=6,所以A1C=8.
所以${V_{{A_1}-BCD}}={V_{D-{A_1}BC}}=\frac{1}{3}×\frac{1}{2}×6×8×6=48$.(14分)
点评 本题考查直线与平面垂直的判定与性质吗,平面与平面垂直的判定定理的应用,几何体的体积的求法,考查逻辑推理以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目