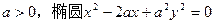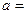题目内容
(本小题满分14分)
过抛物线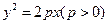 的对称轴上一点
的对称轴上一点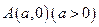 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线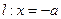 作垂线,垂足分别为
作垂线,垂足分别为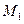 、
、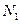 。
。 

(Ⅰ)当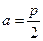 时,求证:
时,求证: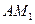 ⊥
⊥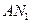 ;
;
(Ⅱ)记
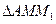 、
、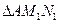 、
、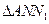 的面积分别为
的面积分别为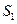 、
、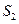 、
、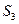 ,是否存在
,是否存在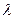 ,使得对任意的
,使得对任意的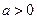 ,都有
,都有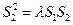 成立。若存在,求出
成立。若存在,求出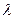 的值;若不存在,说明理由。
的值;若不存在,说明理由。
过抛物线
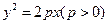 的对称轴上一点
的对称轴上一点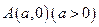 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线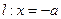 作垂线,垂足分别为
作垂线,垂足分别为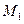 、
、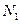 。
。 

(Ⅰ)当
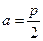 时,求证:
时,求证: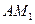 ⊥
⊥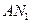 ;
;(Ⅱ)记

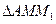 、
、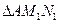 、
、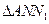 的面积分别为
的面积分别为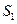 、
、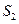 、
、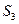 ,是否存在
,是否存在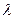 ,使得对任意的
,使得对任意的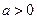 ,都有
,都有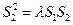 成立。若存在,求出
成立。若存在,求出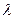 的值;若不存在,说明理由。
的值;若不存在,说明理由。
解 依题意,可设直线MN的方程为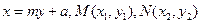 ,
,
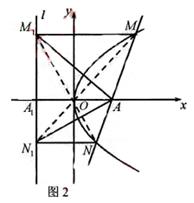
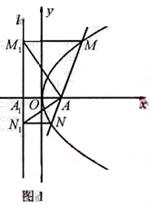
则有
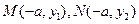
由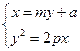 ,消去x可得
,消去x可得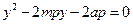


从而有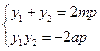 ①
①
于是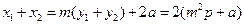 ②
②
又由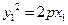 ,
,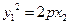 可得
可得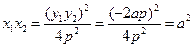 ③
③
(Ⅰ)如图1,当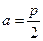 时,点
时,点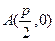 即为抛物线的焦点,
即为抛物线的焦点,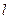 为其准线
为其准线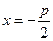
此时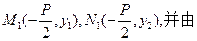 ①可得
①可得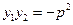
证法1: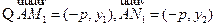
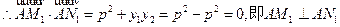


证法2:

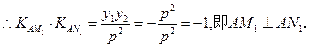


(Ⅱ)存在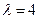 ,使得对任意的
,使得对任意的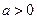 ,都有
,都有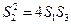 成立,证明如下:
成立,证明如下:
证法1:记直线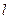 与x轴的交点为
与x轴的交点为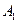 ,则
,则 。于是有
。于是有
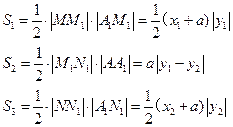


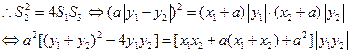
将①、②、③代入上式化简可得
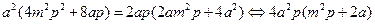
上式恒成立,即对任意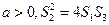 成立
成立 

证法2:如图2,连接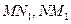 ,则由
,则由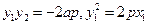 可得
可得
 ,所以直线
,所以直线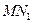 经过原点O,
经过原点O,
同理可证直线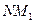 也经过原点O
也经过原点O
又 设
设 则
则
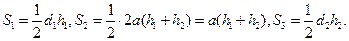
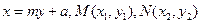 ,
,

则有

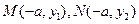
由
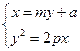 ,消去x可得
,消去x可得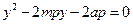


从而有
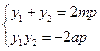 ①
①于是
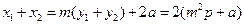 ②
②又由
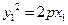 ,
,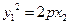 可得
可得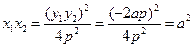 ③
③(Ⅰ)如图1,当
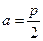 时,点
时,点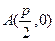 即为抛物线的焦点,
即为抛物线的焦点,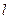 为其准线
为其准线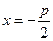
此时
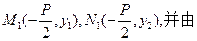 ①可得
①可得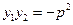
证法1:
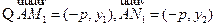
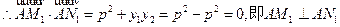


证法2:


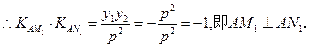


(Ⅱ)存在
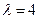 ,使得对任意的
,使得对任意的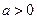 ,都有
,都有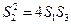 成立,证明如下:
成立,证明如下:证法1:记直线
 与x轴的交点为
与x轴的交点为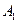 ,则
,则 。于是有
。于是有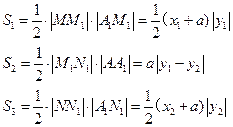


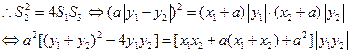
将①、②、③代入上式化简可得
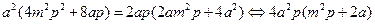
上式恒成立,即对任意
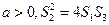 成立
成立 

证法2:如图2,连接
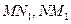 ,则由
,则由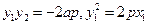 可得
可得 ,所以直线
,所以直线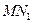 经过原点O,
经过原点O,同理可证直线
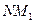 也经过原点O
也经过原点O又
 设
设 则
则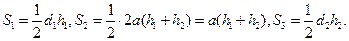

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
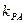 和
和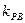 ,且满足
,且满足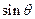 ,
,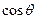 是方程
是方程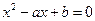 的两根,求点
的两根,求点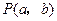 的轨迹方程.
的轨迹方程.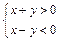 表示的平面区域为
表示的平面区域为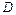 ,区域
,区域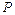 到直线
到直线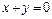 和直线
和直线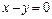 的距离之积为2, 记点
的距离之积为2, 记点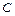 . 是否存在过点
. 是否存在过点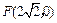 的直线l, 使之与曲线
的直线l, 使之与曲线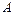 、
、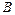 ,且以线段
,且以线段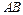 为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.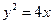 有一个公共焦点,且其离心率是双曲线
有一个公共焦点,且其离心率是双曲线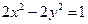 的离心率的倒数,
的离心率的倒数,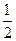 )是直线
)是直线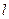 被椭圆截得的线段的中点,求直线
被椭圆截得的线段的中点,求直线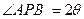 ,且
,且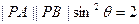 . (I)求动点P的轨迹G的方程;(II)过点B的直线
. (I)求动点P的轨迹G的方程;(II)过点B的直线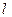 与轨迹G交于两点M,N.试问在x轴上是否存在定点C ,使得
与轨迹G交于两点M,N.试问在x轴上是否存在定点C ,使得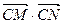 为常数.若存在,求出点C的坐标;若不存在,说明理由.
为常数.若存在,求出点C的坐标;若不存在,说明理由.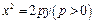 上的两个动点,
上的两个动点,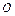 为坐标原点,非零向量
为坐标原点,非零向量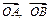 满足
满足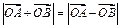 .
.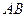 经过一定点;
经过一定点;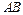 的中点到直线
的中点到直线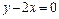 的距离的最小值为
的距离的最小值为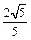 时,求
时,求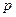 的值.
的值.